1) (25s^3 - 9s^2 + 2s - 11) + (9s^2 + 11) 2) (-7x^2 + 14) + (10x + 7 - 5x^2) 3) (9a^8 - a^2 - 3a^5 - a^4 - a) 4) (33n^4 + 7n^2 + 10n^3) + (3n^4 + 19n^5 + n + 6n^2 + 2n^3) 5) (11c^5... 1) (25s^3 - 9s^2 + 2s - 11) + (9s^2 + 11) 2) (-7x^2 + 14) + (10x + 7 - 5x^2) 3) (9a^8 - a^2 - 3a^5 - a^4 - a) 4) (33n^4 + 7n^2 + 10n^3) + (3n^4 + 19n^5 + n + 6n^2 + 2n^3) 5) (11c^5 - 25c - 4c^4 + 3c^2 + C^6) + (-7c^3 - 2c^4 + 15c)
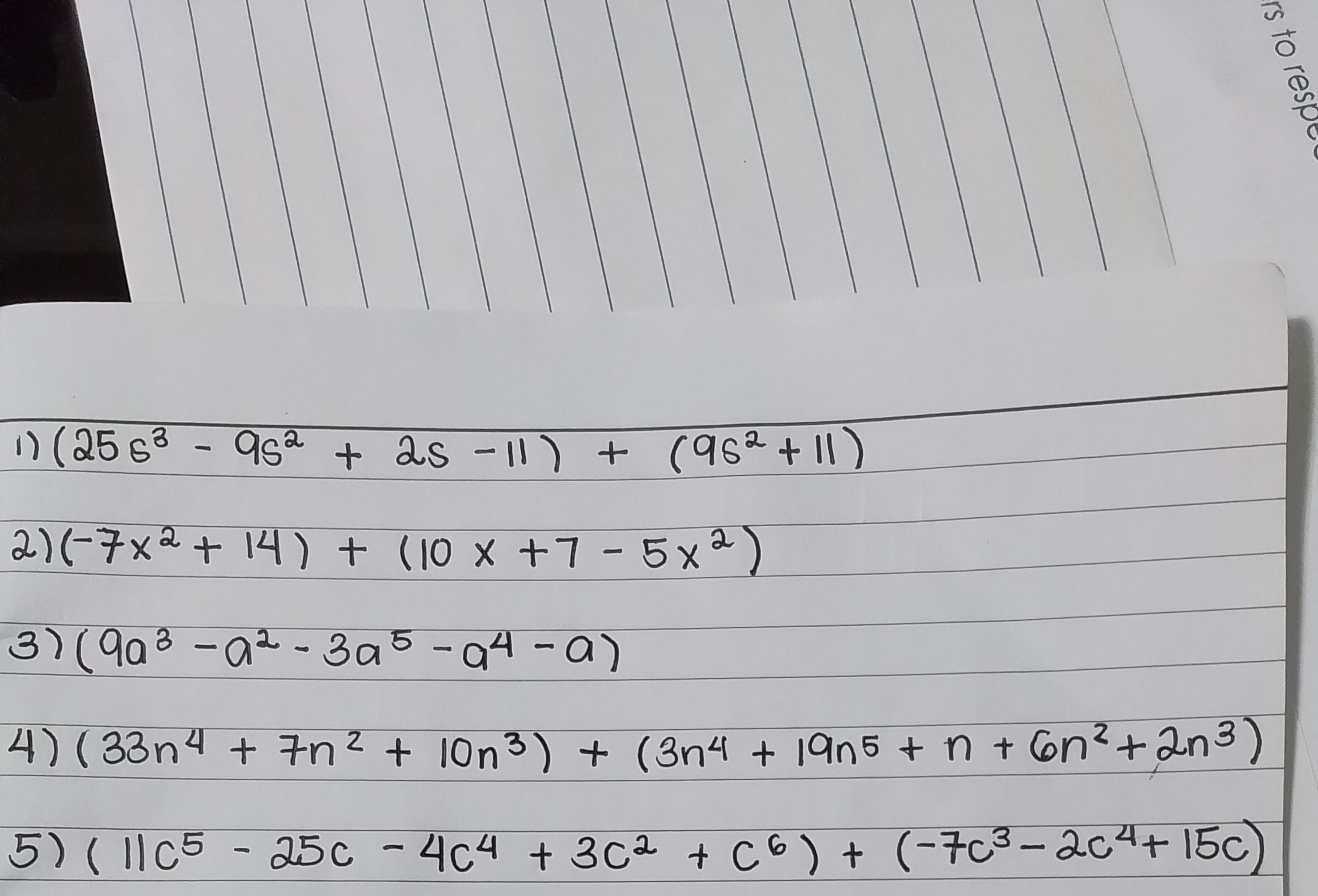
Understand the Problem
The question consists of multiple polynomial expressions that require simplification through addition and/or multiplication. Each item involves combining like terms and correctly working through the arithmetic.
Answer
1. $25s^3 + 2s$ 2. $-12x^2 + 10x + 21$ 3. $9a^8 - a^2 - 3a^5 - a^4 - a$ 4. $19n^5 + 36n^4 + 12n^3 + 13n^2 + n$ 5. $c^6 + 11c^5 - 6c^4 - 7c^3 + 3c^2 - 10c$
Answer for screen readers
- $$25s^3 + 2s$$
- $$-12x^2 + 10x + 21$$
- $$9a^8 - a^2 - 3a^5 - a^4 - a$$
- $$19n^5 + 36n^4 + 12n^3 + 13n^2 + n$$
- $$c^6 + 11c^5 - 6c^4 - 7c^3 + 3c^2 - 10c$$
Steps to Solve
-
Simplify the First Expression
Start with the first expression:
$$(25s^3 - 9s^2 + 2s - 11) + (9s^2 + 11)$$
Combine like terms:
- The $s^3$ term: $25s^3$
- The $s^2$ terms: $-9s^2 + 9s^2 = 0$
- The $s$ terms: $2s$
- The constant terms: $-11 + 11 = 0$
Result:
$$25s^3 + 2s$$
-
Simplify the Second Expression
Now for the second expression:
$$(-7x^2 + 14) + (10x + 7 - 5x^2)$$
Combine like terms:
- The $x^2$ terms: $-7x^2 - 5x^2 = -12x^2$
- The $x$ terms: $10x$
- The constant: $14 + 7 = 21$
Result:
$$-12x^2 + 10x + 21$$
-
Simplify the Third Expression
For the third expression:
$$(9a^8 - a^2 - 3a^5 - a^4 - a)$$
There are no like terms to combine. Thus, the result is:
$$9a^8 - a^2 - 3a^5 - a^4 - a$$
-
Simplify the Fourth Expression
For the fourth expression:
$$(33n^4 + 7n^2 + 10n^3) + (3n^4 + 19n^5 + n + 6n^2 + 2n^3)$$
Combine like terms:
- The $n^5$ term: $19n^5$
- The $n^4$ terms: $33n^4 + 3n^4 = 36n^4$
- The $n^3$ terms: $10n^3 + 2n^3 = 12n^3$
- The $n^2$ terms: $7n^2 + 6n^2 = 13n^2$
- The constant term: $n$
Result:
$$19n^5 + 36n^4 + 12n^3 + 13n^2 + n$$
-
Simplify the Fifth Expression
For the fifth expression:
$$(11c^5 - 25c - 4c^4 + 3c^2 + c^6) + (-7c^3 - 2c^4 + 15c)$$
Combine like terms:
- The $c^6$ term: $c^6$
- The $c^5$ term: $11c^5$
- The $c^4$ terms: $-4c^4 - 2c^4 = -6c^4$
- The $c^3$ term: $-7c^3$
- The $c^2$ term: $3c^2$
- The $c$ terms: $-25c + 15c = -10c$
Result:
$$c^6 + 11c^5 - 6c^4 - 7c^3 + 3c^2 - 10c$$
- $$25s^3 + 2s$$
- $$-12x^2 + 10x + 21$$
- $$9a^8 - a^2 - 3a^5 - a^4 - a$$
- $$19n^5 + 36n^4 + 12n^3 + 13n^2 + n$$
- $$c^6 + 11c^5 - 6c^4 - 7c^3 + 3c^2 - 10c$$
More Information
These results show the simplified form of each set of polynomial expressions. Each polynomial combines like terms effectively and maintains a standard order based on the degree of terms.
Tips
- Failing to combine all like terms, especially the constants or coefficients.
- Miscalculating signs when combining terms (e.g., mixing positive and negative signs).
- Not properly organizing terms before adding or subtracting.
AI-generated content may contain errors. Please verify critical information