Déterminer les valeurs de la moyenne et de l'écart type. Trouver les intervalles de confiance de ces paramètres à 90%. Estimer la pluie décennale et son intervalle de confiance à 8... Déterminer les valeurs de la moyenne et de l'écart type. Trouver les intervalles de confiance de ces paramètres à 90%. Estimer la pluie décennale et son intervalle de confiance à 80%.
Understand the Problem
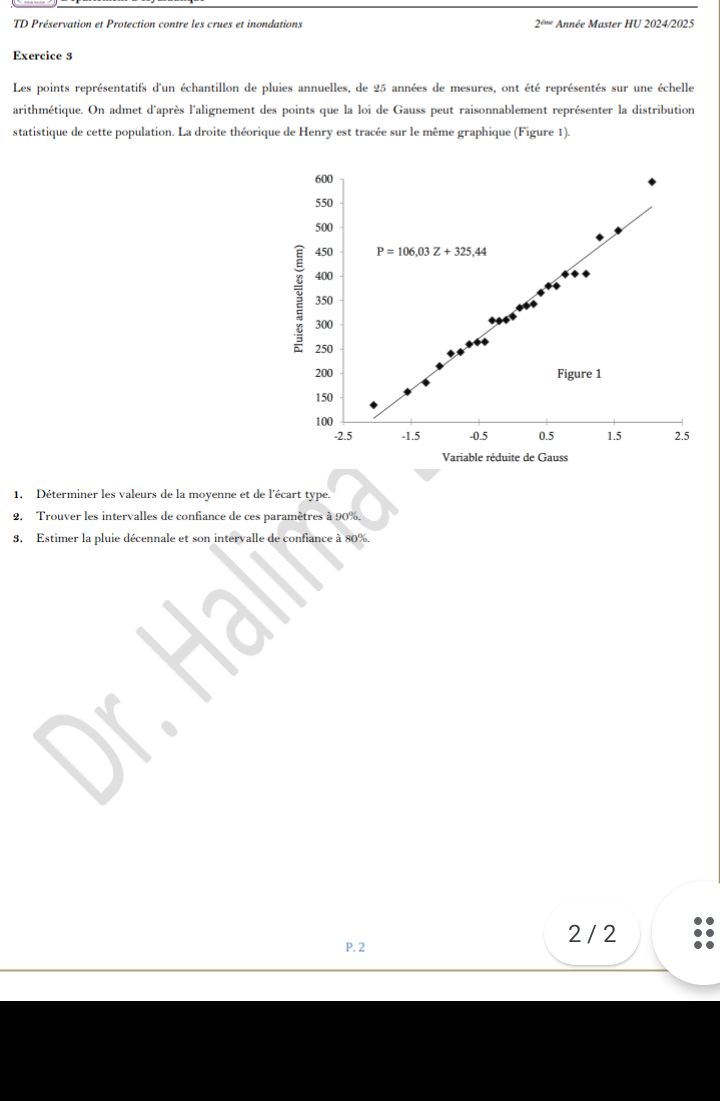
La question demande de déterminer la moyenne et l'écart type d'un échantillon de données de pluie, de trouver les intervalles de confiance pour ces paramètres, et d'estimer la pluie décennale avec son intervalle de confiance. Cela implique des concepts statistiques tels que la moyenne, l'écart type, et l'estimation des intervalles de confiance.
Answer
La moyenne est $ \bar{P} $, l'écart type est $ \sigma $, et les intervalles de confiance pour la moyenne et la pluie décennale sont à calculer avec les formules appropriées.
Answer for screen readers
La moyenne est $ \bar{P} $ (à calculer avec les données) et l'écart type est $ \sigma $ (à calculer avec les données). Les intervalles de confiance doivent être déterminés en fonction des valeurs de z et des calculs effectués. L'estimation de la pluie décennale et son intervalle de confiance doivent aussi être calculés.
Steps to Solve
- Calculer la moyenne (m) des données de pluie
Pour calculer la moyenne, additionnez toutes les observations de pluie (P) et divisez par le nombre total d'observations (n):
$$ \bar{P} = \frac{\sum_{i=1}^{n} P_i}{n} $$
- Calculer l'écart type (σ)
L'écart type se calcule en utilisant la formule suivante :
$$ \sigma = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(P_i - \bar{P})^2} $$
où $P_i$ sont les valeurs individuelles et $\bar{P}$ est la moyenne calculée précédemment.
- Déterminer les intervalles de confiance à 90% pour la moyenne
L'intervalle de confiance pour la moyenne est calculé à l'aide de la formule :
$$ IC = \bar{P} \pm z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} $$
où $z_{\alpha/2}$ est la valeur critique pour un intervalle de confiance de 90%.
- Estimer la pluie décennale et son intervalle de confiance à 80%
Pour estimer la pluie décennale, vous pouvez utiliser la moyenne et ajuster par la fréquence décennale, puis calculer l'intervalle de confiance de la même manière que pour la moyenne, en utilisant un niveau de confiance de 80%.
$$ IC_{décennale} = P_{10} \pm z_{0.10} \cdot \frac{\sigma}{\sqrt{10}} $$
La moyenne est $ \bar{P} $ (à calculer avec les données) et l'écart type est $ \sigma $ (à calculer avec les données). Les intervalles de confiance doivent être déterminés en fonction des valeurs de z et des calculs effectués. L'estimation de la pluie décennale et son intervalle de confiance doivent aussi être calculés.
More Information
Il est important de considérer que pour des échantillons plus petits, l'utilisation de la distribution t est plus appropriée. Cela affecte les valeurs critiques utilisées pour les intervalles de confiance. Les résultats peuvent varier en fonction de la qualité et de la distribution des données.
Tips
- Oublier de vérifier si les données suivent une distribution normale peut conduire à utiliser des méthodes inappropriées.
- Ne pas ajuster pour le nombre de degrés de liberté lors du calcul de l'écart type.
- Mélanger les valeurs critiques pour différents niveaux de confiance.
AI-generated content may contain errors. Please verify critical information