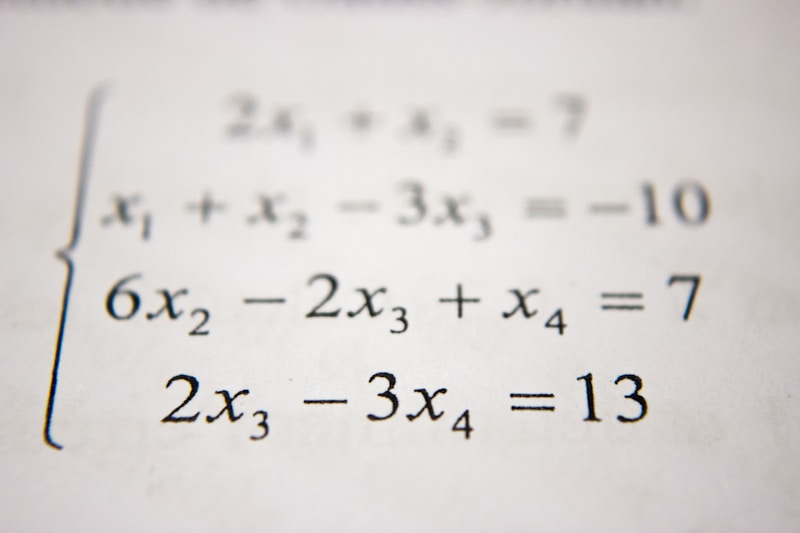10 Questions
A linear equation can involve variables, coefficients, constants, and arithmetic operations.
True
In algebraic expressions, the pattern describes relationships between quantities using only numerical values.
False
A quadrilateral always has more than 4 sides.
False
Real numbers include only integers and whole numbers.
False
Expanding binomials is a technique used in solving linear equations.
False
A rhombus is a type of quadrilateral with all sides equal in length.
True
Linear equations in two variables always have a unique solution.
False
The number 0.0 is classified as an irrational number.
False
Squares and rectangles are examples of parallelograms.
True
Real numbers include only integers and fractions, excluding decimal approximations.
False
Study Notes
Maths Essentials: Algebraic Expressions, Quadrilaterals, Real Numbers, Linear Equations
Mathematics is a universal language, encompassing various concepts used to describe our world and solve practical problems. This exploration will delve into four essential facets of math—algebraic expressions, quadrilaterals, real numbers, and linear equations—to expand your understanding and appreciation of these foundational subjects.
Algebraic Expressions
Algebraic expressions are constructed from variables, coefficients, constants, and arithmetic operations like addition, subtraction, multiplication, and division. They typically follow a pattern that describes relationships between quantities, enabling us to represent and manipulate them symbolically rather than relying solely on numerical values. For example, 3x + 6 represents a relationship where adding six times some variable 'x' yields any given value when x is substituted with specific numbers.
An expression can involve parentheses, exponentiation, and other mathematical operators to create complex structures that help express solutions to various problems. Developments in this area allow students to solve more advanced problems using techniques such as factoring, combining like terms, and expanding binomials.
Quadrilaterals
A quadrilateral is a plane shape consisting of four sides and four vertices (corners) connected by line segments. Some common types of quadrilaterals include squares, rectangles, parallelograms, trapezoids, rhombuses, and kites. Understanding their properties helps us visualize geometric shapes, identify similarities and differences among them, and apply concepts like symmetry, perimeter, area, and congruence in problem solving.
Quadrilateral geometry provides insights into theoretical mathematics while also serving as building blocks for exploring more complicated polygons. By learning and applying definitions, formulas, and proofs related to this subject domain, one acquires valuable skills necessary for comprehending higher mathematics.
Real Numbers
Real numbers constitute a broad set including integers (-∞ ... -1, 0, 1, 2...), fractions (such as $\frac{1}{2}$), decimal approximations (like 3.14159), irrational numbers (e.g., $\sqrt{2}$, (\pi)), and special cases like negative zero ((-0)) and positive zeros (like 0.0). Mastery over this concept allows mathematicians and students to perform precise calculations, compare magnitudes, and order elements along the number line.
In real analysis, we examine the behavior of functions defined on intervals containing real numbers; hence, it's crucial to understand basic arithmetic properties and operations with real numbers before diving deeper into calculus and its applications.
Linear Equations
Linear equations in two variables have the general format (ax+by=c), where (a,\ b,\ c) are constants and (x) and (y) are unknown variables. Solving systems of linear equations helps determine unique, independent, dependent, inconsistent, or infinitely many solutions based on the nature of the system and its components. These equations lay the foundation for graphing, data modeling, and economic analyses.
Understanding how linear equations work enables students to recognize patterns, make predictions, and develop critical thinking abilities fundamental to career success across numerous fields. Moreover, forming connections between abstract theories and concrete applications strengthens intuition and reasoning capabilities throughout the study of mathematics.
Explore the fundamental concepts of algebraic expressions, quadrilaterals, real numbers, and linear equations in mathematics. Enhance your understanding of relationships between variables, geometric shapes, number sets, and systems of equations through this comprehensive exploration.
Make Your Own Quizzes and Flashcards
Convert your notes into interactive study material.