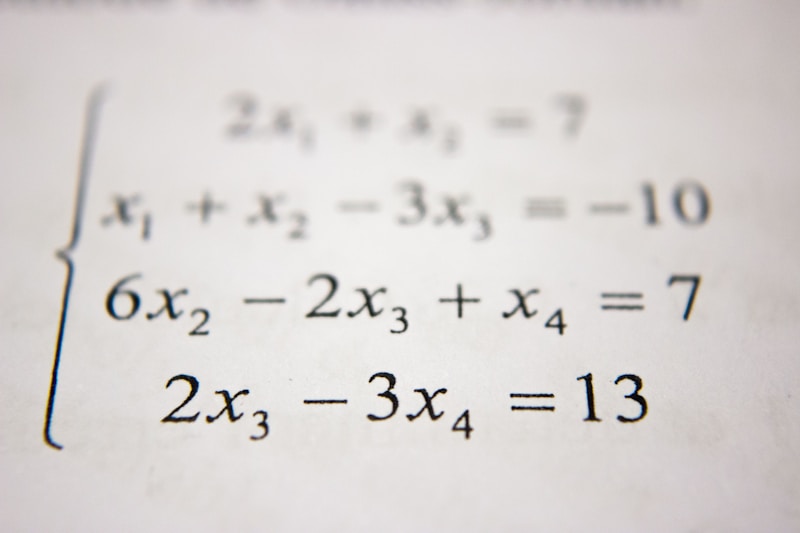Questions and Answers
Which of the following is NOT a scientific discipline that relies on calculus?
Sociology
The fundamental theorem of calculus states that differentiation and integration are _____.
Inverse processes
If we have a velocity function $v(t)$, we can use differential calculus to find the _____.
Acceleration
Which of the following is a primary focus of integral calculus?
Signup and view all the answers
Who were the two mathematicians credited with independently developing calculus in the 17th century?
Signup and view all the answers
What mathematical notation is used to find the area under a curve in integral calculus?
Signup and view all the answers
In physics, which areas can calculus be applied to?
Signup and view all the answers
What was one of the limitations of pre-calculus methods in finding areas under curves?
Signup and view all the answers
Which field relies on calculus to estimate risks and probabilities in insurance and finance?
Signup and view all the answers
In what way did the development of differential calculus enhance mathematicians' capabilities?
Signup and view all the answers
Study Notes
Introduction
Calculus is a branch of mathematics that deals with the calculation of instantaneous rates of change and the summation of infinitely many small factors. It is often regarded as the foundation for many scientific disciplines, including physics, chemistry, biology, economics, finance, and actuarial science. Calculus was independently developed by two mathematicians, Isaac Newton of England and Gottfried Wilhelm Leibniz of Germany, in the 17th century. Today, calculus has become an essential tool for solving problems in various fields.
Differential Calculus
The branch of calculus concerned with differential calculus deals with instantaneous rates of change. It involves finding the derivative of a function, which represents the slope of a curve at any given point. This branch of calculus helps us understand how the value of a function changes when its input changes. For example, if we have a velocity function v(t), we can use differential calculus to find the acceleration a(t) = dv(t)/dt, representing the rate at which the velocity is changing over time.
Integral Calculus
Integral calculus is another major branch of calculus that focuses on summing infinitely many small factors. It allows us to calculate areas under curves, volumes of solids, and work done by physical systems. The fundamental theorem of calculus states that differentiation and integration are inverse processes; thus, finding integrals is equivalent to solving certain types of differential equations. In integral calculus, we can find the area under a curve by using the definite integral notation ∫ from x = a to x = b, where f(x) is the function describing the curve and dx indicates the increment of x over which the function is being integrated.
Applications of Calculus
Calculus has widespread applications in various scientific disciplines. For instance, in physics, calculus can be used to describe the motion of objects and solve problems related to gravitation, fluid dynamics, electromagnetism, and quantum mechanics. In engineering, calculus provides the foundation for structural analysis, control theory, and optimization techniques. Economists rely on calculus to analyze markets, optimize production and consumption, and model economic systems. Actuarial science uses calculus to estimate risks and probabilities in insurance and finance.
Calculating Curves and Areas
Before the development of calculus, finding areas under curves was solved using geometric techniques like Archimedes' method for approximating the area of a parabolic segment. However, with the advent of differential calculus, mathematicians could describe motion algebraically, which allowed them to not only find areas but also calculate velocities, slopes, and other derivatives.
Conclusion
Calculus is a powerful mathematical tool that has revolutionized our understanding of the world around us. From the smallest particles to the vastness of the universe, calculus provides insights into continuous change and helps us solve complex problems in various fields. With its rich history and wide range of applications, calculus remains an indispensable part of modern mathematics.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
Explore the fundamentals of calculus, including differential calculus for rates of change and integral calculus for summing infinitesimally small factors. Learn how calculus revolutionized various scientific disciplines and its wide-ranging applications in physics, engineering, economics, and actuarial science.