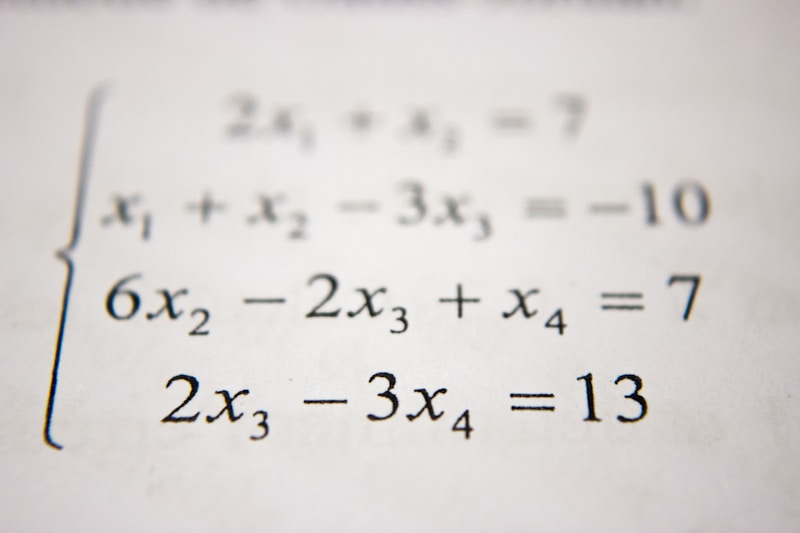Questions and Answers
In algebra, what do the intersection points in solving systems of linear equations represent?
Solutions
What technique involves multiplying or dividing both sides of an equation by a constant to isolate variables?
Multiplication and Division of Equations
Which mathematical method is often used to find approximate or exact solutions to polynomial equations?
Rational Root Theorem
In what branch of Maths do we use algebra to calculate forces, moments, velocities, and accelerations in engineering designs and physics experiments?
Signup and view all the answers
Who among the ancient mathematicians is credited with introducing the concept of solving algebraic equations using letters to represent unknowns?
Signup and view all the answers
Which ancient text is considered to be the foundation of modern algebra?
Signup and view all the answers
What is the fundamental concept that algebra deals with?
Signup and view all the answers
What are algebraic expressions composed of?
Signup and view all the answers
What is the distinguishing feature of linear equations?
Signup and view all the answers
Study Notes
Exploring the Wonders of Maths: A Comprehensive Guide to Algebra
Maths, the enchanting world of numbers and patterns, has captivated the minds of humans for millennia. Among its many branches, algebra stands as a foundational and indispensable tool that tames the complexities of mathematical concepts. Let's embark on a journey to unravel the richness of algebra and its vital role in the broader realm of Maths.
Algebra: The Language of Maths
Algebra is the branch of Maths that deals with solving symbolic expressions and equations, and it has its roots in the works of ancient Greek mathematicians like Diophantus, who wrote the famous Arithmetica in the 3rd century AD. This book introduced the concept of solving algebraic equations using letters to represent unknowns and is considered the foundation of modern algebra.
Algebraic Expressions
An algebraic expression refers to a combination of constants and variables that are connected using mathematical operations like addition, subtraction, multiplication, and division. For example, 2x + 5y is an algebraic expression, where x and y represent variables while 2 and 5 are constants.
Linear Equations
Linear equations are the simplest form of algebraic expressions, where the highest exponent of the variable is 1. These equations can be represented in the form ax + b = c, where a, b, and c are constants, and x is the variable. Solving linear equations is a fundamental skill in algebra, as they are foundational in many real-world problems.
Solving Algebraic Equations
Solving algebraic equations involves manipulating expressions to isolate variables and find the value(s) that make the equation true. There are several techniques for solving equations, including the following:
-
Simplifying expressions: Combining like terms to simplify expressions, e.g.,
3x + 5 + 2x = (3 + 2)x + 5 = 5x + 5. -
Addition and Subtraction of Equations: Adding or subtracting similar equations to isolate variables, e.g.,
2x + 3 = 5and2x - 1 = 4. Adding these equations, we get3 = 6 - 1 → 2x = 5 → x = 5/2. -
Multiplication and Division of Equations: Multiplying or dividing both sides of an equation by a constant to isolate variables, e.g.,
3x + 2 = 10→3x = 8 → x = 8/3.
Systems of Linear Equations
A system of linear equations consists of two or more equations that involve the same variables. Solving systems of linear equations often involves using techniques like substitution, elimination, or graphing to find the intersection points, which represent the solutions.
Quadratic Equations
Quadratic equations are algebraic expressions of the form ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. Solving quadratic equations can be done using factoring, completing the square, or the quadratic formula.
Polynomial Equations
Polynomial equations are algebraic expressions of the form a_nx^n + a_(n-1)x^{n-1} + ... + a_1x + a_0 = 0, where a_n, a_(n-1), ..., a_1, and a_0 are constants, and x is the variable. Solving polynomial equations can be challenging, and often, we rely on numerical methods like Newton-Raphson or the Rational Root Theorem to find approximate or exact solutions.
Applications of Algebra in Real-World Problems
Algebra plays a pivotal role in solving a wide array of real-world problems, including:
- Financial Applications: Calculating loan payments, determining compound interest, and budgeting expenses, to name a few.
- Physics and Engineering: Calculating forces, moments, velocities, and accelerations in engineering designs and physics experiments.
- Biology and Medicine: Analyzing the effects of drug concentrations, understanding population growth rates, and interpreting epidemiological data.
In summary, algebra is a fascinating and indispensable branch of Maths that equips us with the tools to solve complex problems and interpret the world around us. It provides a crucial foundation for countless real-world applications and paves the way for further mathematical breakthroughs. Regardless of whether you're a seasoned mathematician or a beginner, a deeper understanding of algebra is an essential step towards mastering the beauty and complexity of Maths.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
Embark on a comprehensive journey through algebra, the indispensable language of mathematical expressions and equations. Explore the intricacies of algebraic expressions, linear equations, systems of linear equations, quadratic equations, polynomial equations, and the wide array of real-world applications of algebra in fields like finance, physics, engineering, biology, and medicine.