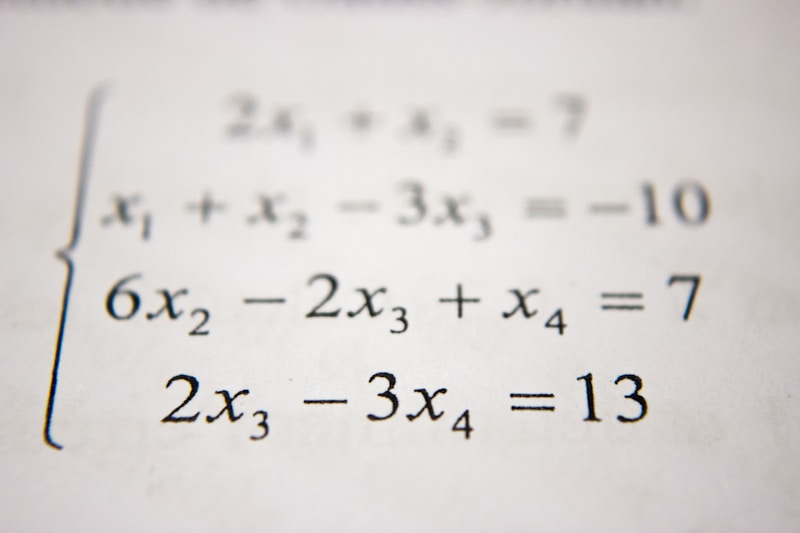Exploring Algebra: Fundamental Concepts and Applications

Exploring Maths: Delving into Algebra

When we think about mathematics, one subtopic that stands out is algebra, a branch of mathematics that deals with the manipulation of symbols and expressions. Algebra is a fundamental building block of mathematics and forms an indispensable part of our daily lives, whether through solving equations, analyzing data, or understanding scientific concepts.

Algebraic Expressions

In algebra, we often deal with expressions that involve symbols, such as variables (e.g., x, y, z) and constants (e.g., 5, 7, π). These expressions can represent the unknown quantities in mathematical problems. For example, consider the expression 3x + 2y. Here, x and y are variables representing unknown quantities, while 3 and 2 are constants.

Operators and Equations

Operators are symbols that perform operations on mathematical expressions. Algebra uses various operators, such as addition (+), subtraction (-), multiplication (*), division (/), exponentiation (^), and modulus (%). We use these operators to construct and manipulate algebraic expressions.

Equations are the core of algebraic problems. An equation is an expression that asserts that two expressions are equal, such as 5x + 2 = 13. To solve an algebraic problem, we use mathematical rules and operations to isolate the variable(s) on one side of an equation.

Linear Equations

Linear equations are a critical subtopic in algebra. A linear equation is an algebraic expression that can be written in the form ax + b = c, where a, b, and c are constants, and x is the variable. Solving linear equations involves isolating the variable x to find its value.

One of the most common methods to solve linear equations is by using the following rules:

1. Add or subtract expressions from both sides of an equation to eliminate variables or simplify the expression.
2. Multiply or divide both sides of an equation by a constant to eliminate fractions or decimals.
3. Use inverse operations to find the value of the variable by isolating it.

Quadratic Equations

Quadratic equations are another important subtopic in algebra. A quadratic equation is an algebraic expression of the form ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. Solving quadratic equations involves using various techniques, such as factoring, completing the square, or using the quadratic formula.

The quadratic formula is a fundamental equation in algebra, expressed as:

x = (-b ± √(b^2 - 4ac)) / (2a)

Algebraic Applications

Algebra forms the foundation of many fields, such as physics, engineering, and statistics. It is crucial in solving real-world problems by representing and manipulating data, developing models, and making predictions. For instance, algebra plays a significant role in determining the trajectory of a projectile, calculating the amount of medication needed to treat a patient, or analyzing the data collected during an experiment.

Algebraic Software and AI

Thanks to the advancements in technology, we now have tools that can assist us in solving algebraic problems. One such tool is the Bing Chat "No Search" feature, which allows users to have a dialogue with the AI without relying on web search results. This feature is particularly helpful in solving complex mathematical problems, such as those involving algebra.

In conclusion, algebra is a fascinating and essential subtopic in mathematics that allows us to solve equations and manipulate expressions. Its applications range from simple calculations to complex real-world problems. As technology advances, we can now rely on software and AI to help us solve algebraic problems more efficiently and effectively.

Explore the fundamental concepts of algebra, including algebraic expressions, operators, equations, linear equations, quadratic equations, and their real-world applications in physics, engineering, and statistics. Discover how algebraic software and AI tools can assist in solving complex mathematical problems.