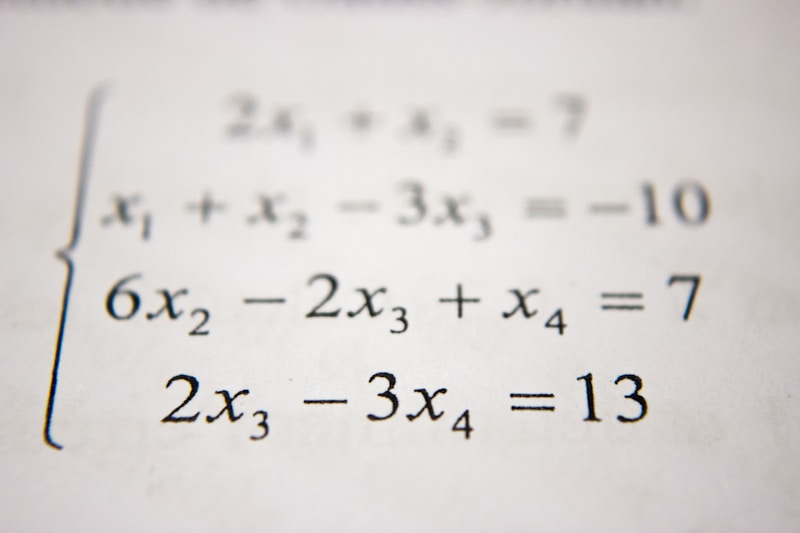Questions and Answers
What is the main purpose of algebraic expressions?
To represent mathematical relationships using numbers and variables
How are variables typically represented in algebraic expressions?
By letters or symbols
What does it mean for two algebraic expressions to be equal in an equation?
The expressions on each side of the equation have the same value for all variable values
Why is simplifying important in solving algebraic equations?
Signup and view all the answers
What is the distinguishing feature of linear equations?
Signup and view all the answers
How are quadratic equations different from linear equations?
Signup and view all the answers
What technique is commonly used to solve quadratic equations?
Signup and view all the answers
What type of expressions are polynomials?
Signup and view all the answers
In the context of linear equations, what is the significance of x = k?
Signup and view all the answers
What makes systems of linear equations challenging to solve?
Signup and view all the answers
Study Notes
Mathematics: Exploring the World of Algebra
Mathematics, often referred to as the "language of science," encompasses a broad range of subjects, including algebra. Algebra, a branch of mathematics that deals with symbols, rules, and relationships, is fundamental to understanding various aspects of mathematics and real-world problems. In this article, we'll explore algebra and its key concepts.
Algebraic Expressions and Equations
An algebraic expression is a combination of numbers, variables, and operations, such as addition, subtraction, multiplication, and division. The variables in an algebraic expression are represented by letters, and the expressions are often written without an equal sign.
For example, consider the expression 2x - 5y + 7. Here, x and y are variables, and the expression is composed of the terms 2x, -5y, and 7.
An algebraic equation is an equation that states that two algebraic expressions are equal. Equations typically include an equal sign (=) to indicate that the expressions on each side are equivalent. For example, 2x - 5y + 7 = 0 is an algebraic equation.
Solving Algebraic Equations
Solving algebraic equations involves finding the values of the variables that make the equation true. There are several methods for solving algebraic equations, such as the following:
- Simplifying: Combine like terms and simplify the expression before solving.
- Isolating variables: Move all terms with one variable to one side of the equation, leaving the other side with only constant terms.
- Matching coefficients: Set coefficients of like terms equal to one another and solve for the variable.
Linear Equations
Linear equations are algebraic equations in which the highest power of any variable is 1. They're often represented as ax + by + c = 0, where a, b, and c are constants, and x is the variable. Linear equations are useful in a wide range of applications, from physics to finance.
Solving linear equations involves isolating the variable to find its value. There are infinite solutions for linear equations, and they're often represented as x = k, where k is the value of x that satisfies the equation.
Systems of Linear Equations
A system of linear equations consists of two or more equations with one or more variables. Solving a system of linear equations can be challenging, but there are several methods to approach the problem, such as substitution, elimination, and matrices.
Quadratic Equations
Quadratic equations are algebraic equations of the form ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. Quadratic equations have one or two solutions, depending on the value of the discriminant (b² - 4ac). To solve quadratic equations, we can use the quadratic formula, factoring, or completing the square.
Polynomials
Polynomials are algebraic expressions that consist of a finite sum of terms, each involving a product of a constant coefficient and one or more variables raised to a non-negative integer power. Polynomials are useful in many areas, such as physics, engineering, and computer science.
In Conclusion
Algebra is a fundamental branch of mathematics that provides essential skills for solving a broad range of problems. The concepts and techniques presented here are only the beginning of the vast world of algebra. Keep exploring algebra, and you'll discover its importance and versatility in our daily lives and the world around us.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
This article delves into the world of algebra, covering algebraic expressions, equations, linear equations, systems of linear equations, quadratic equations, and polynomials. Learn about solving algebraic equations, the importance of linear equations in various fields, methods for solving systems of linear equations, and different techniques for solving quadratic equations and working with polynomials.