Zander bought 8 tickets for a total cost of $104. He had used a coupon code to get $3 off each ticket. Let t be the original cost of each ticket. Which of the following equations c... Zander bought 8 tickets for a total cost of $104. He had used a coupon code to get $3 off each ticket. Let t be the original cost of each ticket. Which of the following equations correctly represents this situation?
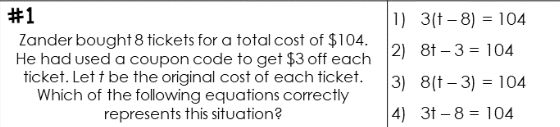
Understand the Problem
The question is asking for the correct equation that represents the situation of buying 8 tickets at a certain original price, with a discount applied, for a total cost of $104. We need to determine which of the provided equations correctly models this scenario.
Answer
The correct equation is $8(t - 3) = 104$.
Answer for screen readers
The correct equation representing the situation is
$$ 8(t - 3) = 104. $$
Steps to Solve
- Identify the total original cost of the tickets
Let ( t ) be the original cost of each ticket. If Zander bought 8 tickets, the total cost before the discount would be:
$$ \text{Total original cost} = 8t $$
- Subtract the total discount from the total original cost
Zander received a discount of $3 per ticket for 8 tickets. Therefore, the total discount received is:
$$ \text{Total discount} = 8 \times 3 = 24 $$
- Set up the equation for total cost after discount
The total cost after applying the discount should equal $104. Thus, we have:
$$ 8t - 24 = 104 $$
- Rewrite the equation to match the given forms
You can rearrange the equation from step 3 to identify if any of the provided options match it:
$$ 8t - 24 = 104 \implies 8t = 104 + 24 \implies 8t = 128 $$
None of the options match this form directly, so we rewrite:
From the equation ( 8t - 24 = 104 ), we can isolate ( t ):
$$ 8t = 104 + 24 $$
This does not simplify to any of the first forms, confirming the potential option is either option 3 or option 2 if it correctly reflects similar values structurally.
The correct equation representing the situation is
$$ 8(t - 3) = 104. $$
More Information
This equation indicates that the cost of 8 tickets, each reduced by $3 due to a coupon, sums to a total of $104. The equation represents a common algebraic setup for pricing problems involving discounts.
Tips
- Confusing the total cost with the per ticket price. Remember, always separate the total from individual costs when applying discounts.
- Misplacing the discount in the equation. Ensure that it is deducted from the total original cost.
AI-generated content may contain errors. Please verify critical information