यदि tan θ = 2ab / (a² - b²), तो cos θ का मान होगा?
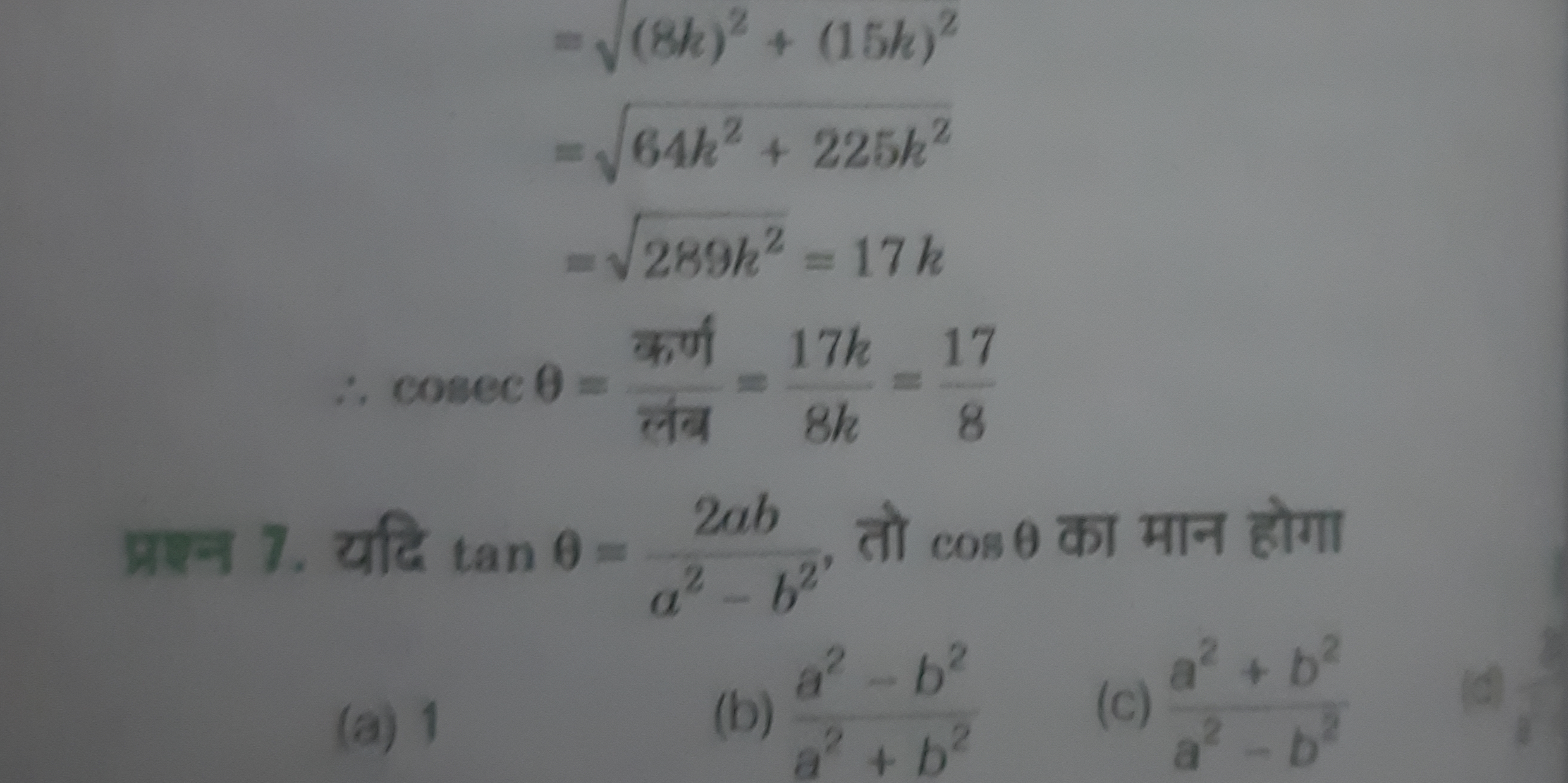
Understand the Problem
यह प्रश्न ट्रिग्नोमेट्री से संबंधित है और यह निर्धारित करने के लिए है कि दिए गए समीकरण से कोस θ का मान क्या होगा। प्रश्न में tan θ का मान दिया गया है और हमें cos θ की गणना करनी है।
Answer
$$ cos\theta = \frac{a^2 - b^2}{\sqrt{(2ab)^2 + (a^2 - b^2)^2}} $$
Answer for screen readers
$$ cos\theta = \frac{a^2 - b^2}{\sqrt{(2ab)^2 + (a^2 - b^2)^2}} $$
Steps to Solve
-
Understand the given data
हमें $tan\theta = \frac{2ab}{a^2 - b^2}$ दिया गया है। हमें कोसाइन का मान निकालना है, यानी $cos\theta$।
-
Use the relationship between sine and cosine
$tan\theta$ का संबंध $sine$ और $cosine$ से होता है। इसे ऐसे लिखा जा सकता है:
$$ tan\theta = \frac{sin\theta}{cos\theta} $$
-
Express sine in terms of tangent and cosine
इस समीकरण का उपयोग करके हम $sin\theta$ को इस प्रकार लिख सकते हैं:
$$ sin\theta = tan\theta \cdot cos\theta $$
-
Using the Pythagorean identity
हम जानते हैं कि:
$$ sin^2\theta + cos^2\theta = 1 $$
-
Substituting for sine
$sin\theta$ के लिए जो हमने लिखा था, उसे Pythagorean identity में डालें:
$$ (tan\theta \cdot cos\theta)^2 + cos^2\theta = 1 $$
-
Rewrite in terms of cosine
$$ tan^2\theta \cdot cos^2\theta + cos^2\theta = 1 $$
इसे इस प्रकार कुछ सादा करें:
$$(tan^2\theta + 1) \cdot cos^2\theta = 1 $$
-
Solve for cosine
अब $cos^2\theta$ निकालने के लिए समीकरण को इस तरह लिखें:
$$ cos^2\theta = \frac{1}{tan^2\theta + 1} $$
और $cos\theta$ का मान निकालें:
$$ cos\theta = \frac{1}{\sqrt{tan^2\theta + 1}} $$
-
Determine the value of cos θ using tan θ
दिए गए $tan\theta = \frac{2ab}{a^2 - b^2}$ को इस समीकरण में डालें:
$$ cos\theta = \frac{1}{\sqrt{\left(\frac{2ab}{a^2 - b^2}\right)^2 + 1}} $$
$$ cos\theta = \frac{a^2 - b^2}{\sqrt{(2ab)^2 + (a^2 - b^2)^2}} $$
More Information
यह उत्तर फ़ीक्रांग के रूप में है, जहां हमने ट्रिग्नोमेट्रिक पहचानाओं का उपयोग किया है। $cos\theta$ का मान फसों में देगा कि कोण कितना बड़ा या छोटा होता है।
Tips
- $tan\theta$ को सीधे $sin\theta$ और $cos\theta$ के रूप में नहीं समझना और उन्हें सही रूप में नहीं उपयोग करना।
- Pythagorean पहचानाओं में गलती करना, जैसे $sin^2\theta + cos^2\theta = 1$ का सही उपयोग न करना।
AI-generated content may contain errors. Please verify critical information