Evalúe el límite dado, si existe: lim (x,y) → (5,-1) (x² + y²)
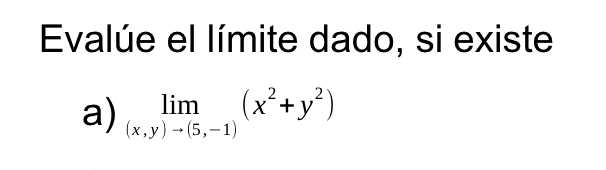
Understand the Problem
La pregunta está pidiendo evaluar un límite en dos variables, específicamente cuando (x, y) se aproxima a (5, -1) para la función x² + y².
Answer
El límite es $26$.
Answer for screen readers
El límite es $26$.
Steps to Solve
- Identificar la función y el punto de evaluación
La función que estamos evaluando es $f(x, y) = x^2 + y^2$. Queremos hallar el límite cuando $(x, y)$ se aproxima a $(5, -1)$.
- Sustitución directa
Para evaluar el límite, sustituimos directamente $(x, y)$ en la función:
$$ f(5, -1) = 5^2 + (-1)^2 $$
- Calcular los valores
Ahora calculamos cada término:
$$ 5^2 = 25 $$
$$ (-1)^2 = 1 $$
- Sumar los resultados
Finalmente, sumamos los resultados obtenidos:
$$ f(5, -1) = 25 + 1 = 26 $$
El límite es $26$.
More Information
Este límite evalúa el comportamiento de la función $f(x, y) = x^2 + y^2$ cuando se aproxima a un punto específico en el plano. Dado que la función es continua, el límite puede ser calculado mediante sustitución directa.
Tips
- Evitar confundir los límites en múltiples variables: Algunos estudiantes pueden intentar evaluar el límite a lo largo de diferentes caminos y concluir incorrectamente. Para funciones continuas, simplemente se puede hacer la sustitución directa.
AI-generated content may contain errors. Please verify critical information