y = x^2 + 8x + 11
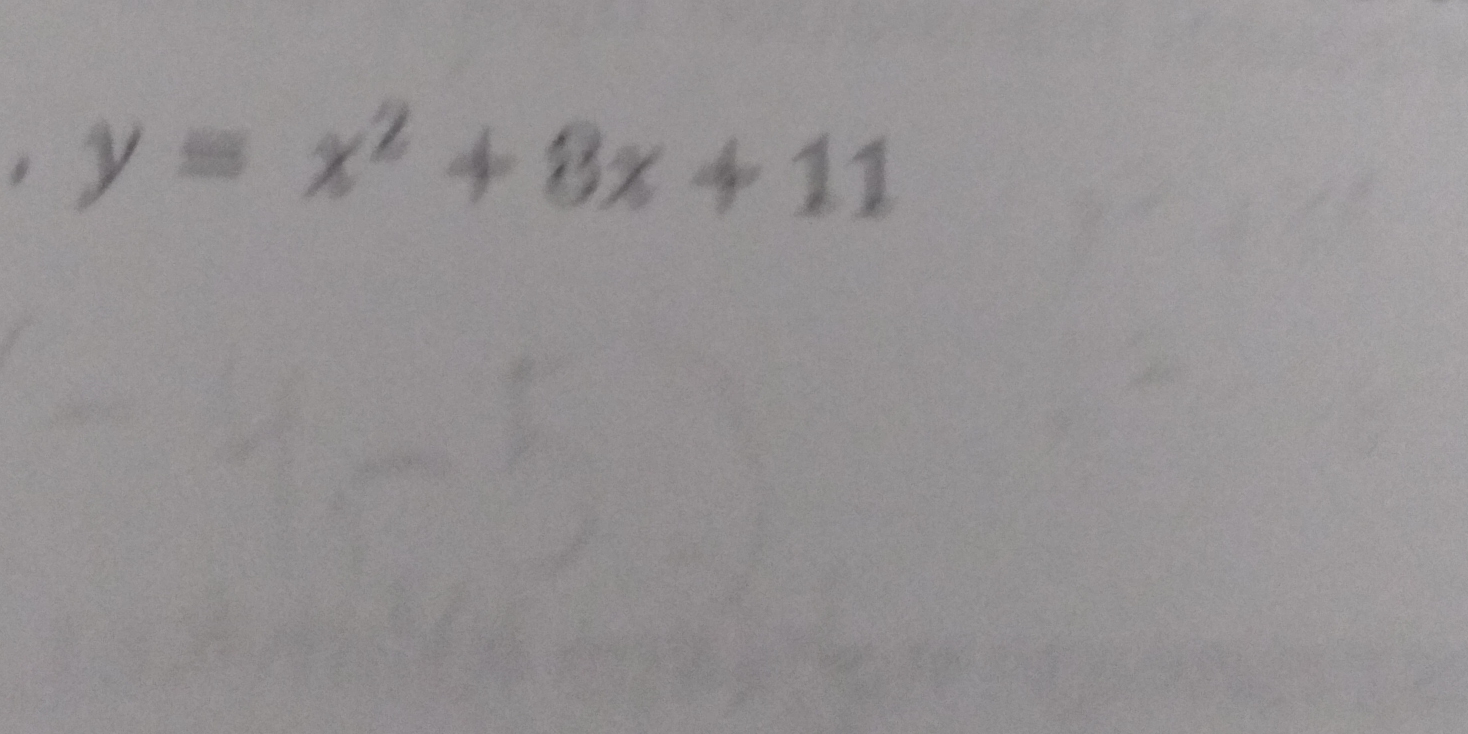
Understand the Problem
The question involves a mathematical expression for a function where y is defined in terms of x. It suggests finding properties or values related to this quadratic equation.
Answer
Vertex: $(-4, -5)$; y-intercept: $(0, 11)$; x-intercepts: $x = -4 \pm \sqrt{5}$.
Answer for screen readers
The vertex of the function is at $(-4, -5)$, the y-intercept is $(0, 11)$, and the x-intercepts are $x = -4 + \sqrt{5}$ and $x = -4 - \sqrt{5}$.
Steps to Solve
- Identify the quadratic function The given function is a quadratic equation of the form $y = ax^2 + bx + c$.
Here, $a = 1$, $b = 8$, and $c = 11$.
-
Find the vertex of the parabola The vertex can be found using the formula for the x-coordinate of the vertex: $$ x = -\frac{b}{2a} $$ Substituting the values, we get: $$ x = -\frac{8}{2 \cdot 1} = -4 $$
-
Calculate the y-coordinate of the vertex Substitute $x = -4$ back into the original equation to find $y$: $$ y = (-4)^2 + 8(-4) + 11 $$ $$ y = 16 - 32 + 11 = -5 $$
-
Summarize the vertex The vertex of the parabola is at the point $(-4, -5)$.
-
Find the y-intercept The y-intercept occurs when $x = 0$. Substituting $x = 0$ into the equation gives: $$ y = 0^2 + 8(0) + 11 = 11 $$ The y-intercept is $(0, 11)$.
-
Find the x-intercepts (if any) To find the x-intercepts, set $y = 0$: $$ 0 = x^2 + 8x + 11 $$ We can use the quadratic formula: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Substituting the values: $$ x = \frac{-8 \pm \sqrt{8^2 - 4 \cdot 1 \cdot 11}}{2 \cdot 1} $$ $$ x = \frac{-8 \pm \sqrt{64 - 44}}{2} $$ $$ x = \frac{-8 \pm \sqrt{20}}{2} $$ $$ x = \frac{-8 \pm 2\sqrt{5}}{2} $$ $$ x = -4 \pm \sqrt{5} $$
Thus, the x-intercepts are $x = -4 + \sqrt{5}$ and $x = -4 - \sqrt{5}$.
The vertex of the function is at $(-4, -5)$, the y-intercept is $(0, 11)$, and the x-intercepts are $x = -4 + \sqrt{5}$ and $x = -4 - \sqrt{5}$.
More Information
The vertex of a quadratic function represents the minimum or maximum point of the parabola, depending on whether it opens upwards or downwards. The y-intercept indicates the point where the graph intersects the y-axis, while the x-intercepts show where it crosses the x-axis.
Tips
- Forgetting to simplify the square root when finding x-intercepts.
- Confusing the vertex form of the quadratic equation with the standard form.
AI-generated content may contain errors. Please verify critical information