y = 4 - x^2, y = 2 - x
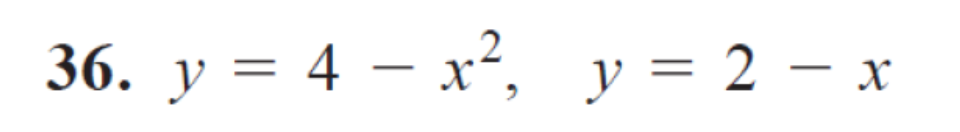
Understand the Problem
The question is asking us to work with two equations, y = 4 - x^2 and y = 2 - x, likely to find their points of intersection or analyze their relationship. This usually involves solving the equations simultaneously.
Answer
No real intersection points between $y = 4 - x^2$ and $y = 2 - x$.
Answer for screen readers
There are no real points of intersection for the equations $y = 4 - x^2$ and $y = 2 - x$.
Steps to Solve
- Set the equations equal to each other
Since both equations equal $y$, we can set them equal to find the points of intersection. $$ 4 - x^2 = 2 - x $$
- Rearrange the equation
To solve for $x$, rearrange the equation so that one side equals zero. $$ x^2 - x + 2 = 0 $$
- Use the quadratic formula
For any quadratic equation of the form $ax^2 + bx + c = 0$, we apply the quadratic formula: $$ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a} $$ In our case, $a = 1$, $b = -1$, and $c = 2$.
- Calculate the discriminant
Calculate the discriminant $D = b^2 - 4ac$. $$ D = (-1)^2 - 4(1)(2) = 1 - 8 = -7 $$
- Determine the nature of the roots
Since the discriminant is negative ($D < 0$), the equations do not intersect, meaning there are no real solutions.
There are no real points of intersection for the equations $y = 4 - x^2$ and $y = 2 - x$.
More Information
The absence of real solutions indicates that the curves represented by these equations do not meet at any point on the Cartesian plane. The quadratic equation derived shows that they may only intersect in complex number space.
Tips
- Forgetting to check the discriminant: Before concluding no intersections, always calculate and analyze the discriminant.
- Misapplying the quadratic formula: Ensure all terms are correctly identified as $a$, $b$, and $c$.
AI-generated content may contain errors. Please verify critical information