x^2 - 8x + 2 = 0

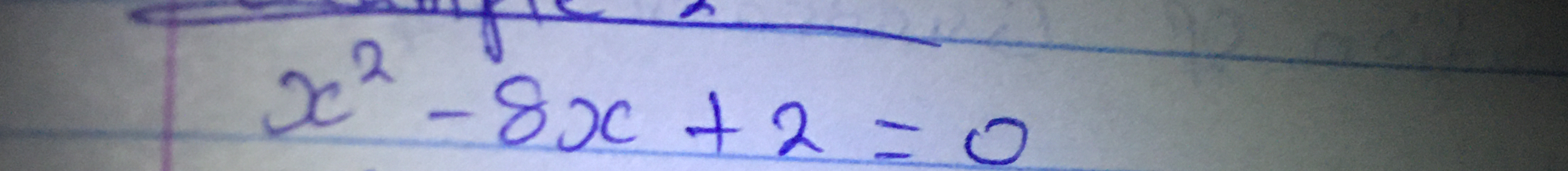
Understand the Problem

The question involves solving a quadratic equation, which is a standard algebraic procedure. We will identify the coefficients and use the quadratic formula or factoring methods to find the values of x.

Answer

The solutions are $x = 4 + \sqrt{14}$ and $x = 4 - \sqrt{14}$.

Steps to Solve

Identify the coefficients
The quadratic equation is given as $x^2 - 8x + 2 = 0$. We identify the coefficients:

$a = 1$ (coefficient of $x^2$)
$b = -8$ (coefficient of $x$)
$c = 2$ (constant term)

Use the quadratic formula
To solve for $x$, we apply the quadratic formula:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Calculate the discriminant
First, calculate $b^2 - 4ac$:
$$ b^2 - 4ac = (-8)^2 - 4 \cdot 1 \cdot 2 = 64 - 8 = 56 $$
Substitute back into the quadratic formula
Now substitute $b$, $a$, and the discriminant into the formula:
$$ x = \frac{-(-8) \pm \sqrt{56}}{2 \cdot 1} $$
This simplifies to:
$$ x = \frac{8 \pm \sqrt{56}}{2} $$
Simplify further
Now simplify $x$:
$$ x = \frac{8 \pm 2\sqrt{14}}{2} $$
This can be simplified to:
$$ x = 4 \pm \sqrt{14} $$
Final solutions
Thus, the solutions for the equation are:
$$ x = 4 + \sqrt{14} \quad \text{and} \quad x = 4 - \sqrt{14} $$

The solutions to the equation are:
$$ x = 4 + \sqrt{14} \quad \text{and} \quad x = 4 - \sqrt{14} $$

More Information

The solutions involve calculating the square root of the discriminant, which in this case is $\sqrt{56}$. This shows the importance of finding factors and simplifying radicals in algebra. The solutions are real and different since the discriminant is positive.

Tips

Neglecting the discriminant: Forgetting to check if the discriminant ($b^2 - 4ac$) is positive, zero, or negative can lead to incorrect conclusions about the nature of the roots.
Simplifying fractions incorrectly: Make sure to cancel correctly when simplifying the fraction in the quadratic formula.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!