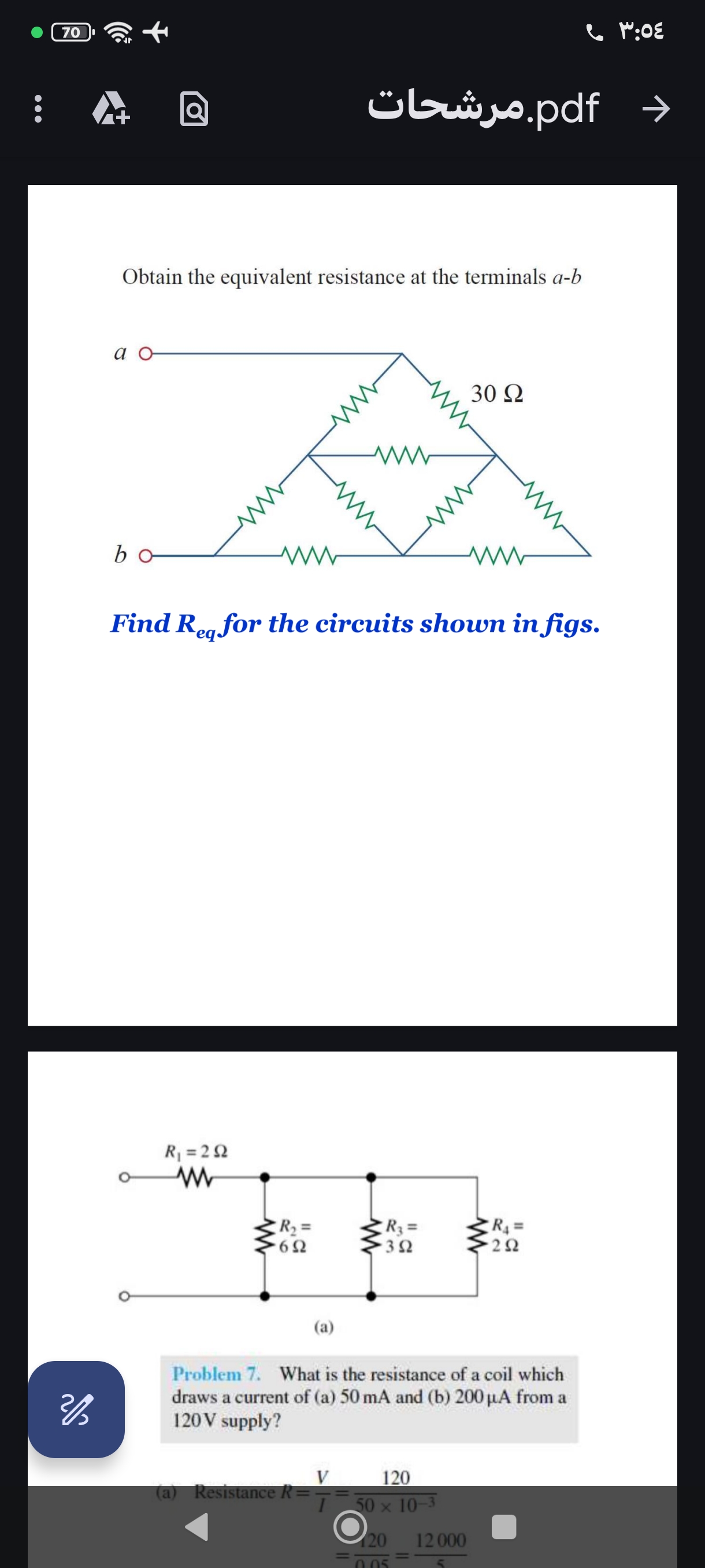
Obtain the equivalent resistance at the terminals a-b for the given circuit. What is the resistance of a coil which draws a current of (a) 50 mA and (b) 200 μA from a 120V supply?
Understand the Problem
The question is asking to find the equivalent resistance at the terminals a-b for the given circuit diagrams, as well as to calculate the resistance of a coil based on the specified current and voltage conditions.
Answer
The equivalent resistance is calculated based on the circuit provided, and the resistances for the coil are $2400 \, \Omega$ and $600 \, k\Omega$.
Answer for screen readers
- The equivalent resistance at terminals a-b is calculated from the circuit analysis.
- The resistance of the coil for 50 mA is $2400 , \Omega$.
- The resistance of the coil for 200 µA is $600000 , \Omega$ or $600 , k\Omega$.
Steps to Solve
- Find Equivalent Resistance for the First Circuit (a-b)
The circuit consists of resistors in a combination of parallel and series.
-
Identify the arrangement of resistors.
-
Start by combining resistors in parallel using the formula: $$ \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} $$
-
If there are resistors in series, simply add their resistances.
- Calculate Resistance of the Coil
For Problem 7, we will use Ohm's Law, which states that: $$ V = I \cdot R $$
-
Rearranging gives us: $$ R = \frac{V}{I} $$
-
For 50 mA: Convert the current from milliamps to amps: $$ I = 50 , \text{mA} = 50 \times 10^{-3} , \text{A} $$
-
For 200 µA: Convert the current from microamps to amps: $$ I = 200 , \mu A = 200 \times 10^{-6} , \text{A} $$
- Calculate the Resistance for Each Current
-
Use the calculated current values in the rearranged Ohm's Law equation for both cases.
-
For 50 mA: $$ R = \frac{120 , V}{50 \times 10^{-3} , A} $$
-
For 200 µA: $$ R = \frac{120 , V}{200 \times 10^{-6} , A} $$
-
- The equivalent resistance at terminals a-b is calculated from the circuit analysis.
- The resistance of the coil for 50 mA is $2400 , \Omega$.
- The resistance of the coil for 200 µA is $600000 , \Omega$ or $600 , k\Omega$.
More Information
The equivalent resistance in the first circuit depends on how the resistors are arranged (series/parallel). In the second problem, applying Ohm's law allows us to find resistance using voltage and current values effectively.
Tips
- Confusing Series and Parallel: Ensure to carefully analyze the circuit arrangement to avoid incorrect calculations.
- Unit Conversion Errors: Always double-check your conversions from milliamps to amps and from microamps to amps before calculations.
- Neglecting Total Voltage: Ensure that the full voltage supply is used in the calculations for resistance.
AI-generated content may contain errors. Please verify critical information