x^2 - 6x + 9 ≤ 0
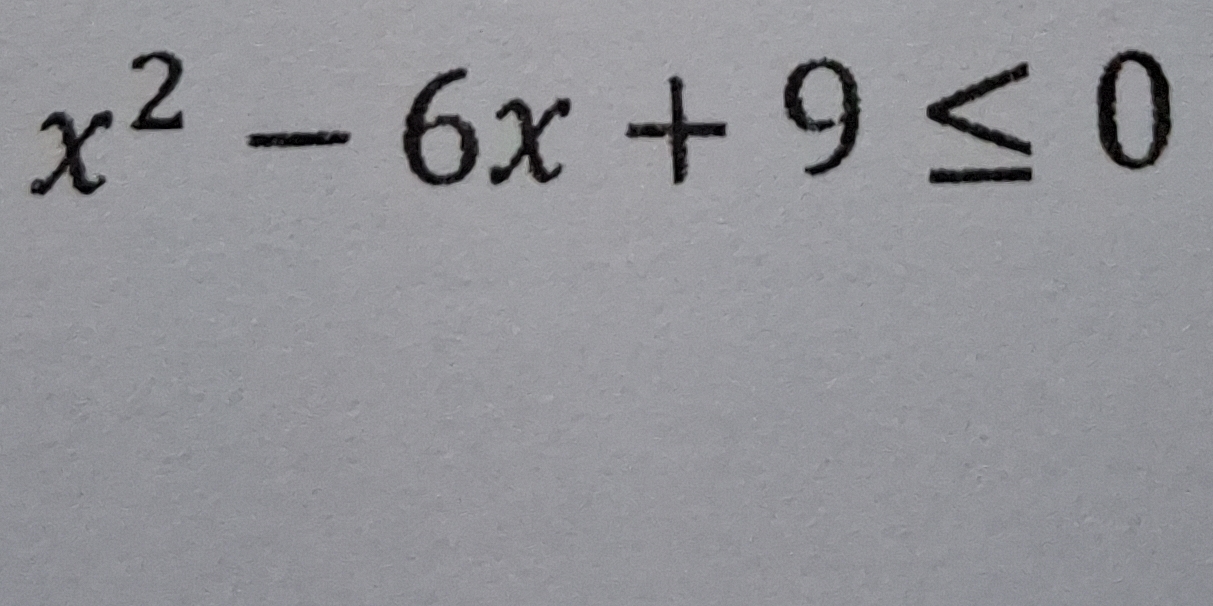
Understand the Problem
The question presents a quadratic inequality that needs to be solved, determining the values of x for which the expression is less than or equal to zero.
Answer
The solution to the inequality is $x = 3$.
Answer for screen readers
The solution to the inequality $x^2 - 6x + 9 \leq 0$ is $x = 3$.
Steps to Solve
- Rewrite the inequality
The inequality is given as $x^2 - 6x + 9 \leq 0$. We can factor the left side.
- Factor the quadratic expression
Notice that $x^2 - 6x + 9$ can be factored as:
$$(x - 3)(x - 3) \leq 0$$
or
$$(x - 3)^2 \leq 0$$
- Analyze the factored form
A square of a number is always non-negative. Therefore, $(x - 3)^2 \geq 0$ for any value of $x$.
- Determine when the expression is zero
The only case when $(x - 3)^2 = 0$ is when:
$$x - 3 = 0 \implies x = 3$$
- Combine the information
From the analysis, $(x - 3)^2$ can only be zero and never negative. Thus, the solution to the inequality is the single point where it equals zero:
$$x = 3$$
The solution to the inequality $x^2 - 6x + 9 \leq 0$ is $x = 3$.
More Information
The expression $x^2 - 6x + 9$ represents a perfect square trinomial. It is a quadratic function that touches the x-axis at $x = 3$ and does not cross it, indicating that the only solution occurs at this point.
Tips
-
Some might incorrectly think that the expression can take negative values. Remember that squares are always non-negative.
-
Confusing the solution set: It’s important to note that solutions to inequalities can consist of intervals or discrete points; in this case, it’s just a single point.
AI-generated content may contain errors. Please verify critical information