∫ (x² + 4x³ + 2) / (6x) dx
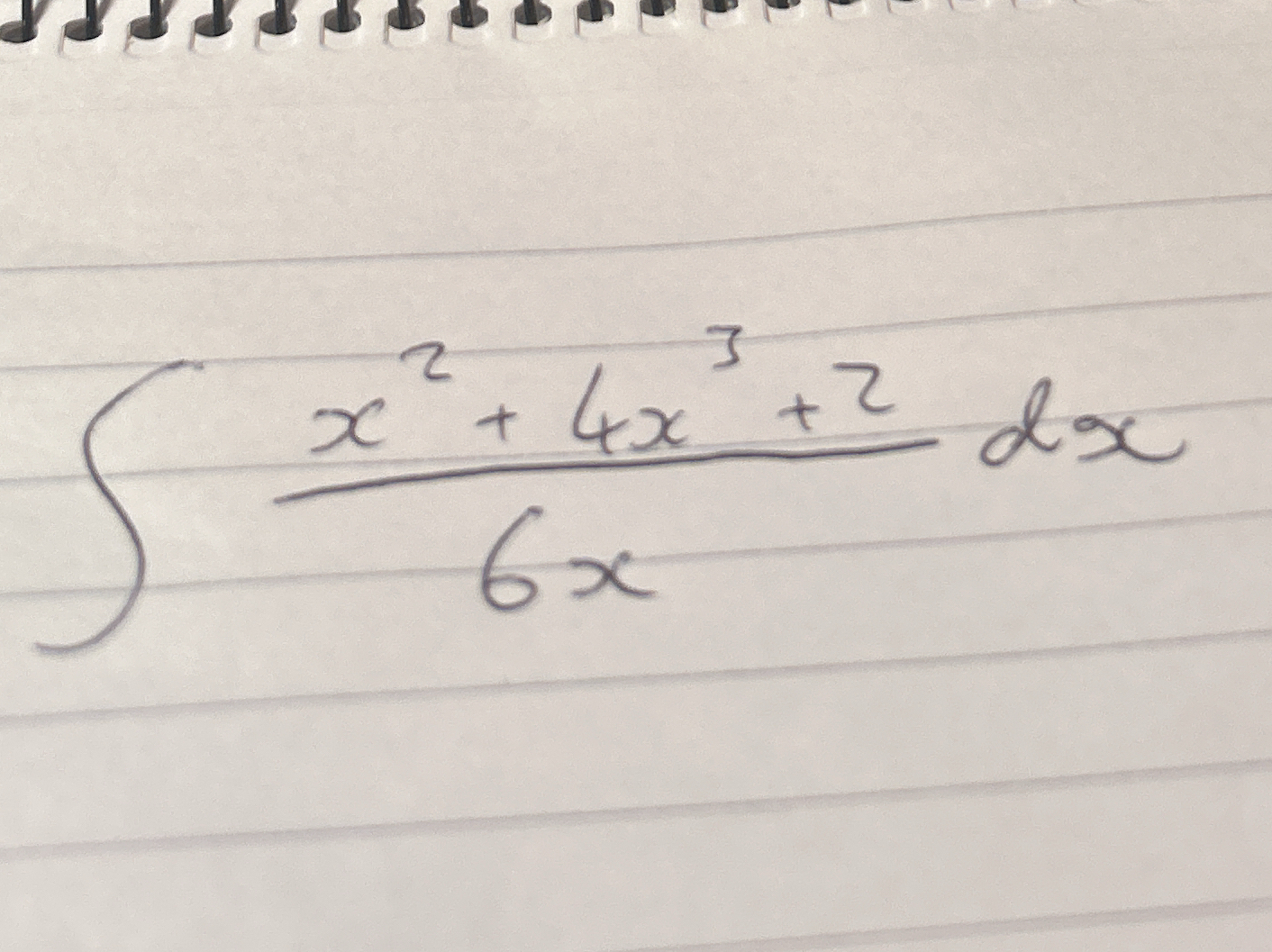
Understand the Problem
The question is asking for the integral of the expression (x² + 4x³ + 2) divided by (6x) with respect to x. This involves simplifying the expression and applying integration techniques.
Answer
The integral evaluates to $$ \frac{x^2}{12} + \frac{2}{9}x^3 + \frac{1}{3} \ln |x| + C $$
Answer for screen readers
The integral of the expression is
$$
\frac{x^2}{12} + \frac{2}{9}x^3 + \frac{1}{3} \ln |x| + C
$$
Steps to Solve
-
Simplify the Expression
We start by rewriting the integrand.
Divide each term of the numerator by the denominator: $$ \frac{x^2}{6x} + \frac{4x^3}{6x} + \frac{2}{6x} = \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} $$ -
Set Up the Integral
Now we can set up the integral with the simplified expression:
$$ \int \left( \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} \right) dx $$ -
Integrate Each Term
We will integrate each term separately:
- The integral of $\frac{x}{6}$ is $\frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12}$.
- The integral of $\frac{2}{3}x^2$ is $\frac{2}{3} \cdot \frac{x^3}{3} = \frac{2}{9}x^3$.
- The integral of $\frac{1}{3x}$ is $\frac{1}{3} \ln |x|$.
Putting it all together, we have: $$ \int \left( \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} \right) dx = \frac{x^2}{12} + \frac{2}{9}x^3 + \frac{1}{3} \ln |x| + C $$
-
Final Result
The final result of the integration is: $$ \frac{x^2}{12} + \frac{2}{9}x^3 + \frac{1}{3} \ln |x| + C $$
The integral of the expression is
$$
\frac{x^2}{12} + \frac{2}{9}x^3 + \frac{1}{3} \ln |x| + C
$$
More Information
Integrals are fundamental in calculus as they represent areas under curves and solutions to differential equations. This integral shows the application of basic integration rules and demonstrates how to handle polynomial and logarithmic functions.
Tips
- Forgetting to simplify the expression before integrating.
- Not applying the logarithmic rule correctly or missing the absolute value in $\ln |x|$.
- Miscalculation during term integration.
