∫ (x² + 4x³ + 2) / (6x) dx
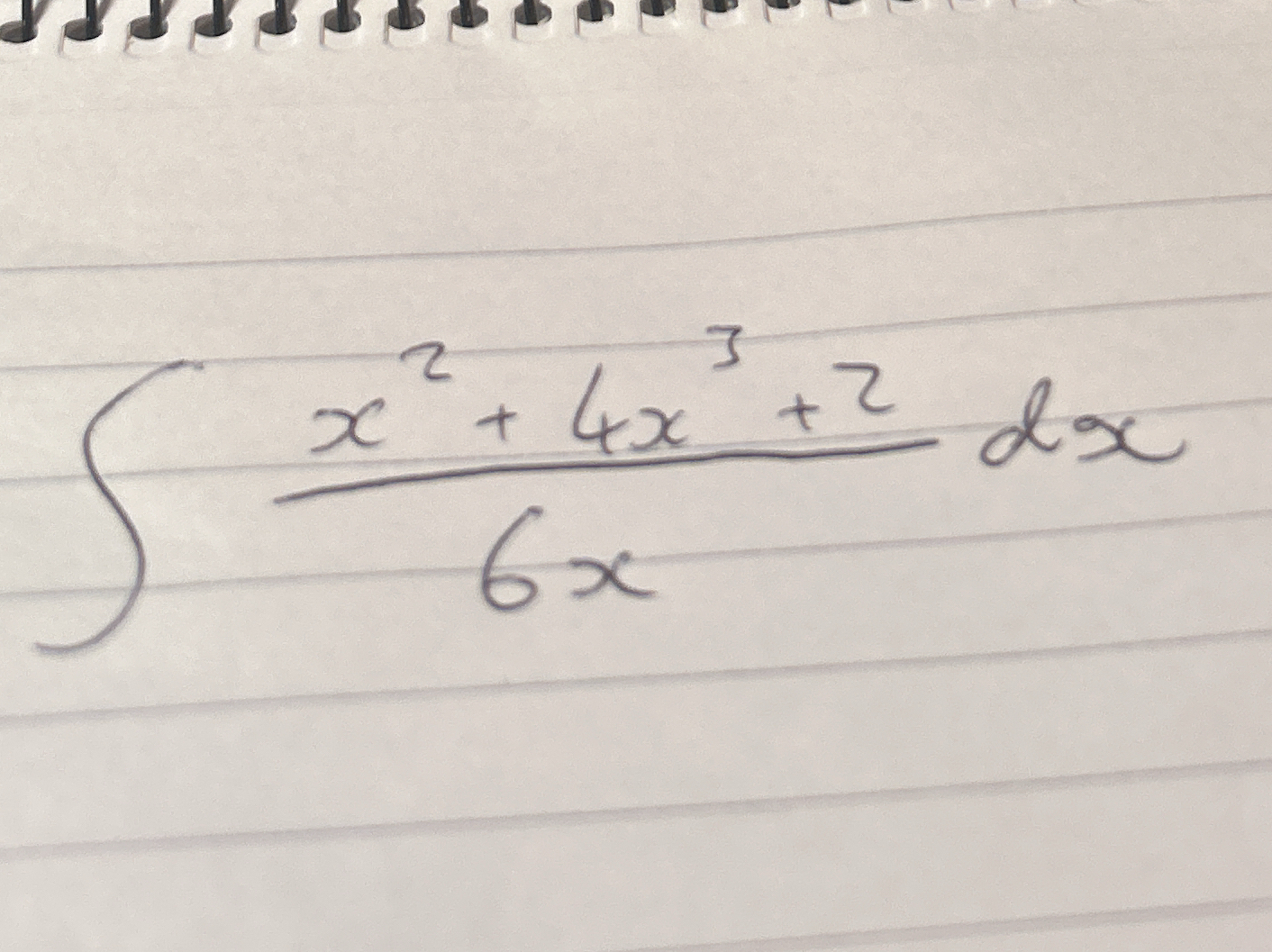
Understand the Problem
The question is asking to evaluate the integral of the expression (x² + 4x³ + 2) / (6x) with respect to x. This involves simplifying the fraction and then performing the integration.
Answer
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Answer for screen readers
The integral evaluates to:
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Steps to Solve
-
Simplify the integrand
First, simplify the fraction:
$$ \frac{x^2 + 4x^3 + 2}{6x} = \frac{x^2}{6x} + \frac{4x^3}{6x} + \frac{2}{6x} $$
This can be simplified further:
$$ = \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} $$
-
Set up the integral
Now, rewrite the integral with the simplified expression:
$$ \int \left( \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} \right) , dx $$
-
Integrate each term
Now, integrate each term:
$$ \int \frac{x}{6} , dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} $$
$$ \int \frac{2}{3}x^2 , dx = \frac{2}{3} \cdot \frac{x^3}{3} = \frac{2x^3}{9} $$
$$ \int \frac{1}{3x} , dx = \frac{1}{3} \ln |x| $$
-
Combine the results
Combine the results of the integrals:
$$ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
where (C) is the constant of integration.
The integral evaluates to:
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
More Information
This result shows the integration of a polynomial divided by a linear term and involves power and logarithmic integration techniques. The constant (C) represents any constant since the original function can have various antiderivatives.
Tips
- Failing to simplify the fraction properly before integration. Always simplify first to make integration easier.
- Not remembering the integral of (\frac{1}{x}), which is (\ln|x|). Ensure you apply the correct rules for logarithmic integration.
AI-generated content may contain errors. Please verify critical information