ln(x^2 - 13x + 36) + 2ln(x - 4) - ln(x - 9)
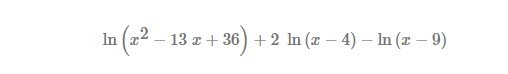
Understand the Problem
The question presents a mathematical expression involving natural logarithms, which we need to simplify or solve. The expression includes logarithmic properties that we will use to combine and simplify the terms.
Answer
The simplified expression is $\ln((x - 4)^3)$.
Answer for screen readers
The simplified expression is: $$ \ln((x - 4)^3) $$
Steps to Solve
- Apply the power rule to the second term
Using the power rule of logarithms, $a \ln(b) = \ln(b^a)$, we can rewrite the second term: $$ 2 \ln(x - 4) = \ln((x - 4)^2) $$
- Combine the logarithmic terms
Now substitute the rewritten term back into the expression: $$ \ln(x^2 - 13x + 36) + \ln((x - 4)^2) - \ln(x - 9) $$ Using the property $\ln(a) + \ln(b) = \ln(ab)$, we combine the first two logarithmic terms: $$ \ln((x^2 - 13x + 36)(x - 4)^2) $$
- Apply the quotient rule
Now, apply the quotient rule for logarithms, $\ln(a) - \ln(b) = \ln \left( \frac{a}{b} \right)$: $$ \ln\left(\frac{(x^2 - 13x + 36)(x - 4)^2}{x - 9}\right) $$
- Simplifying the expression
Next, we need to factor $x^2 - 13x + 36$ to combine or simplify further. The factors of this quadratic are $(x - 4)(x - 9)$. Thus, we can rewrite our expression: $$ \ln\left(\frac{(x - 4)(x - 9)(x - 4)^2}{x - 9}\right) $$
- Final simplification
Simplifying the fraction, the $x - 9$ in the numerator and denominator cancels out: $$ \ln((x - 4)^3) $$
The simplified expression is: $$ \ln((x - 4)^3) $$
More Information
This logarithmic expression represents a power of a single term, making it easier to evaluate or further manipulate in contexts such as derivatives or integrals if needed.
Tips
- Forgetting to apply the power rule when simplifying logarithmic expressions.
- Not correctly applying the properties of logarithms, such as combining logarithmic terms using addition and subtraction rules.
AI-generated content may contain errors. Please verify critical information