∫ (x² + 4)/x² dx
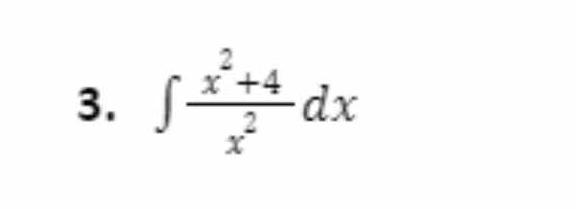
Understand the Problem
The question is asking for the integral of the function (x² + 4)/x² with respect to x. We will solve this by simplifying the integrand and then integrating the resulting expression.
Answer
The integral evaluates to: $x - \frac{4}{x} + C$.
Answer for screen readers
The result of the integral is:
$$
x - \frac{4}{x} + C
$$
Steps to Solve
-
Simplify the Integrand
Begin by simplifying the expression inside the integral:
$$ \frac{x^{2}+4}{x^{2}} = \frac{x^{2}}{x^{2}} + \frac{4}{x^{2}} = 1 + \frac{4}{x^{2}} $$ -
Rewrite the Integral
Now rewrite the integral using the simplified expression:
$$ \int \left(1 + \frac{4}{x^{2}}\right) dx $$ -
Integrate Each Term
Break down the integral into two simpler integrals:
$$ \int 1 , dx + \int \frac{4}{x^{2}} , dx $$ -
Calculate the Integrals
Integrate each part:
-
For the first part:
$$ \int 1 , dx = x $$ -
For the second part, recall that:
$$ \int \frac{1}{x^{n}} , dx = -\frac{1}{n-1} x^{1-n} $$
So, for $\frac{4}{x^{2}}$:
$$ \int \frac{4}{x^{2}} , dx = 4 \left(-\frac{1}{1} x^{-1}\right) = -\frac{4}{x} $$
-
Combine the Results
Now combine the results of both integrals:
$$ x - \frac{4}{x} + C $$
where $C$ is the constant of integration.
The result of the integral is:
$$
x - \frac{4}{x} + C
$$
More Information
This integral illustrates the method of breaking down complex expressions into simpler parts for easier integration. The constant of integration ($C$) is essential because any constant could've been present before differentiation.
Tips
- Forgetting the constant of integration: Always remember to add $C$ to signify the general solution.
- Misapplying the power rule: Ensure to correctly apply the integration rule for powers of $x$.
AI-generated content may contain errors. Please verify critical information