виріши методом мінімальної вартості
Understand the Problem
Запит стосується рішення задачі методом мінімальних витрат, яка, ймовірно, пов'язана з транспортною задачею в операційних дослідженнях. Ми повинні знайти оптимальний розподіл ресурсів між різними варіантами.
Answer
Оптимальний розподіл ресурсів, в якому загальні витрати будуть мінімальні, можна знайти, застосувавши метод мінімальних витрат з урахуванням обмежень постачання та попиту.
Answer for screen readers
Оптимальний розподіл ресурсів, який мінімізує загальні витрати перевезення, буде вказано в знайденій оптимальній матриці розподілу.
Steps to Solve
- Визначення матриці витрат
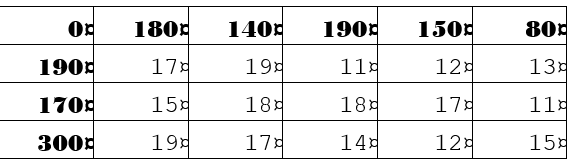
Перший крок — скласти матрицю витрат, що показує витрати на перевезення одиниці вантажу з однієї точки до іншої.
Матриця витрат виглядає наступним чином:
[ \begin{array}{c|cccccc} & 0 & 180 & 140 & 190 & 150 & 80 \ \hline 190 & 17 & 19 & 11 & 12 & 13 \ 170 & 15 & 18 & 18 & 17 & 11 \ 300 & 19 & 17 & 14 & 12 & 15 \ \end{array} ]
- Визначення обмежень
Визначте обмеження для постачання та попиту на кожному з пунктів. Наприклад:
- Постачання: 190, 170, 300
- Попит: 0, 180, 140, 190, 150, 80
- Використання методу потенціалів
Використовуйте метод потенціалів для визначення оптимального розподілу. Спочатку обчисліть початковий базисний розв’язок, застосовуючи метод "першого приближення" (наприклад, метод найбільшого зниження).
- Оцінка залишків
Перевірте, чи є можливість зменшити загальні витрати за рахунок зміни маршруту перевезення. Визначте, чи можна зменшити витрати, перевроджуючи вантажі.
- Оптимізація
Здійсніть кілька ітерацій, поки не отримаєте оптимальний розподіл ресурсів, який мінімізує витрати на перевезення.
Оптимальний розподіл ресурсів, який мінімізує загальні витрати перевезення, буде вказано в знайденій оптимальній матриці розподілу.
More Information
Цей підрахунок дозволить знизити витрати на перевезення товарів, що є важливим у логістиці та управлінні запасами.
Tips
- Неправильне складання витрат на транспортування.
- Ігнорування обмежень постачання та попиту.
- Несвоєчасне перевіряння можливостей оптимізації, що може призвести до неефективних рішень.
AI-generated content may contain errors. Please verify critical information