∫(x² + 4x + 7) / (6x) dx
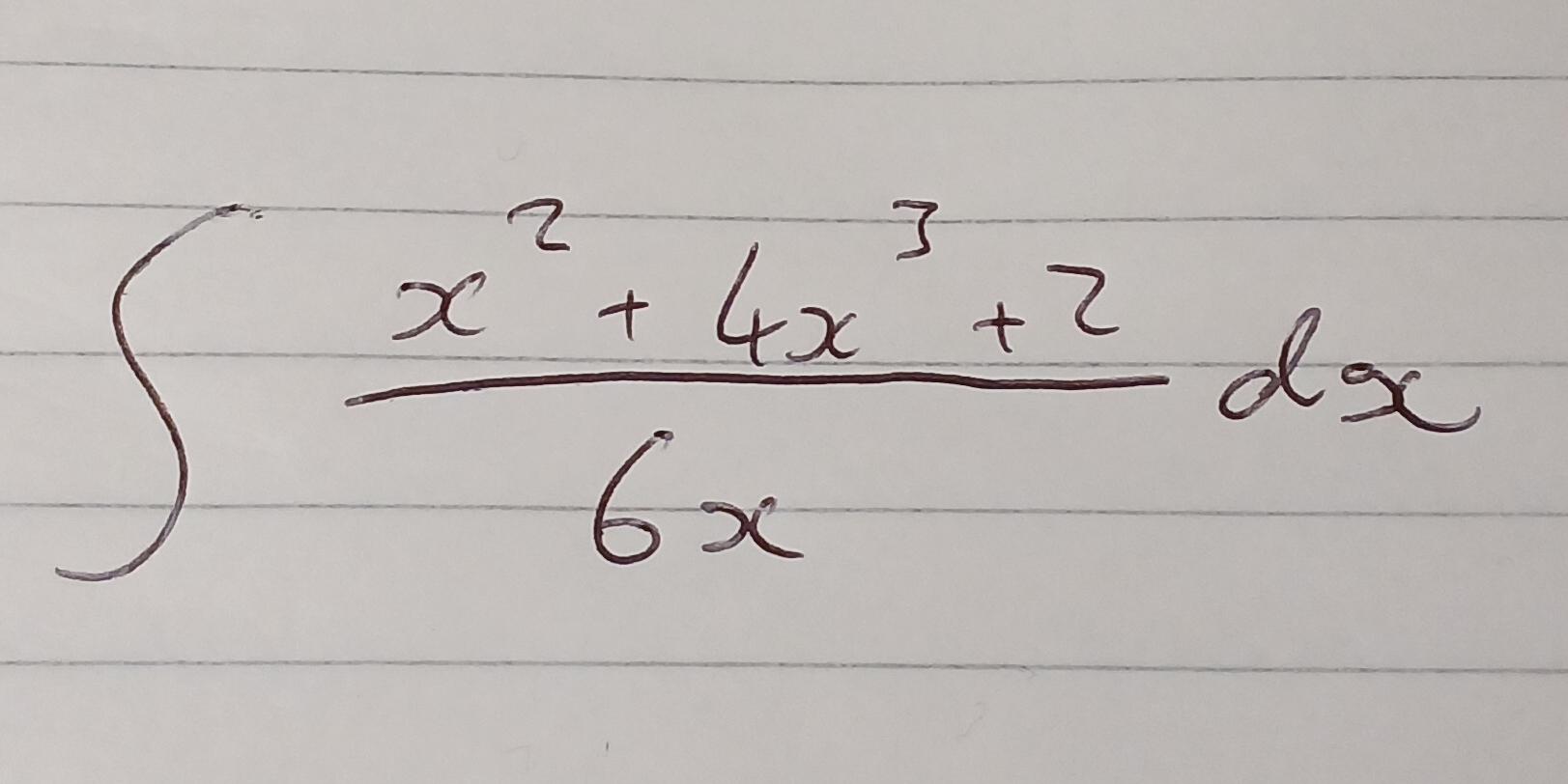
Understand the Problem
The question is asking for the integral of the rational function given by the expression (x^2 + 4x + 7) / (6x) with respect to x. To solve this, we will likely need to simplify the expression before integrating.
Answer
The integral is: $$ \int \frac{x^2 + 4x + 7}{6x} \, dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{7}{6} \ln|x| + C $$
Answer for screen readers
The integral is: $$ \int \frac{x^2 + 4x + 7}{6x} , dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{7}{6} \ln|x| + C $$
Steps to Solve
-
Simplify the Rational Function
Start by dividing each term in the numerator by the denominator: $$ \frac{x^2 + 4x + 7}{6x} = \frac{x^2}{6x} + \frac{4x}{6x} + \frac{7}{6x} $$ This simplifies to: $$ \frac{x}{6} + \frac{2}{3} + \frac{7}{6x} $$
-
Set up the Integral
Rewrite the integral with the simplified expression: $$ \int \left( \frac{x}{6} + \frac{2}{3} + \frac{7}{6x} \right) , dx $$
-
Integrate Each Term
Now, integrate each term individually:
-
For the first term: $$ \int \frac{x}{6} , dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} $$
-
For the second term: $$ \int \frac{2}{3} , dx = \frac{2}{3} x $$
-
For the third term: $$ \int \frac{7}{6x} , dx = \frac{7}{6} \ln|x| $$
-
-
Combine the Results
Combine all the integrated terms and add the constant of integration $C$: $$ \int \frac{x^2 + 4x + 7}{6x} , dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{7}{6} \ln|x| + C $$
The integral is: $$ \int \frac{x^2 + 4x + 7}{6x} , dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{7}{6} \ln|x| + C $$
More Information
Integrating rational functions often involves simplifying them before applying integration techniques. The presence of the natural logarithm arises when integrating functions of the form $\frac{1}{x}$.
Tips
- Forgetting to include the constant of integration $C$.
- Incorrectly simplifying the rational function before integrating.
- Confusing the integration rules, especially for logarithmic terms.
AI-generated content may contain errors. Please verify critical information