∫ (x^2 + 4x + 7) / (6x) dx
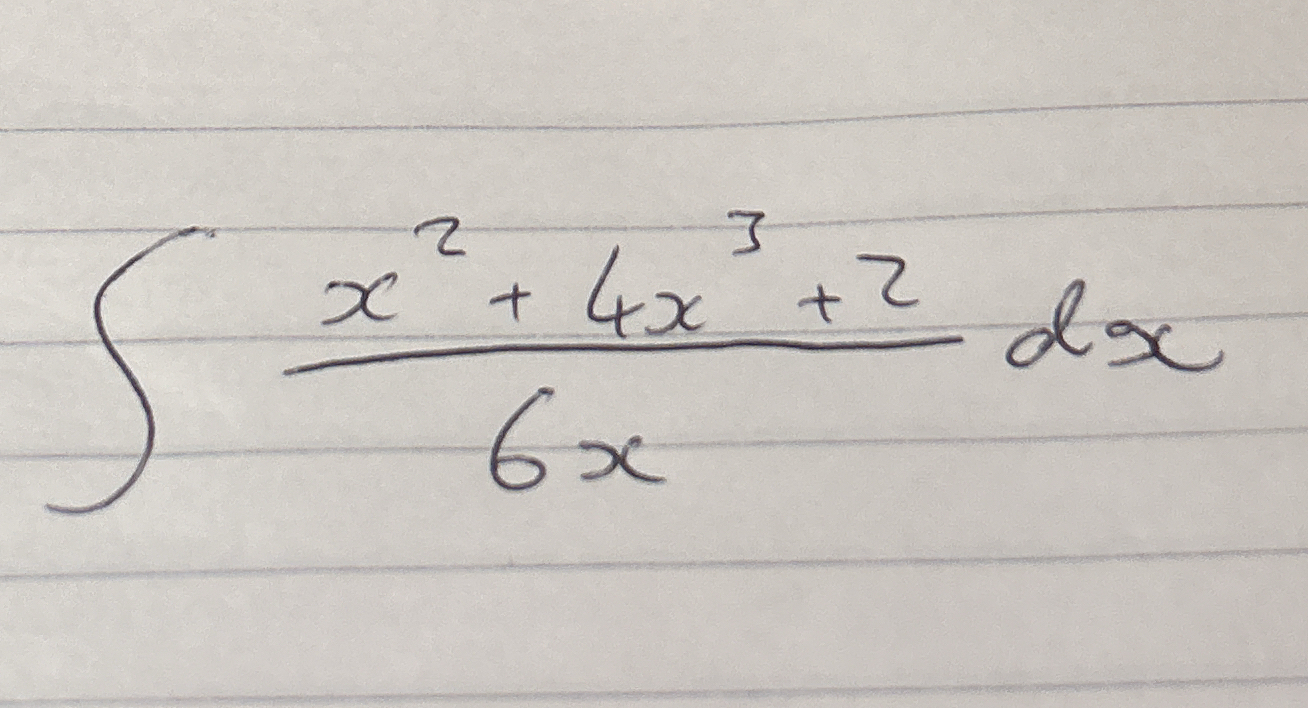
Understand the Problem
The question involves finding the integral of a rational function. Specifically, it asks for the indefinite integral of the polynomial expression divided by 6x with respect to x.
Answer
$$ \int \frac{x^2 + 4x + 7}{6x} \; dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{7}{6} \ln|x| + C $$
Answer for screen readers
$$ \int \frac{x^2 + 4x + 7}{6x} ; dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{7}{6} \ln|x| + C $$
Steps to Solve
- Divide the Polynomial by the Denominator
We start by simplifying the integral:
$$ \int \frac{x^2 + 4x + 7}{6x} ; dx = \int \left(\frac{x^2}{6x} + \frac{4x}{6x} + \frac{7}{6x}\right) dx $$
This simplifies to:
$$ \int \left(\frac{x}{6} + \frac{2}{3} + \frac{7}{6x}\right) dx $$
- Integrate Each Term Separately
Now we can integrate each term in the expression:
- The integral of $\frac{x}{6}$ is:
$$ \int \frac{x}{6} ; dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} $$
- The integral of $\frac{2}{3}$ is:
$$ \int \frac{2}{3} ; dx = \frac{2}{3} x $$
- The integral of $\frac{7}{6x}$ is:
$$ \int \frac{7}{6x} ; dx = \frac{7}{6} \ln|x| $$
- Combine the Results
Putting all components together, we get:
$$ \int \frac{x^2 + 4x + 7}{6x} ; dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{7}{6} \ln|x| + C $$
where ( C ) is the constant of integration.
$$ \int \frac{x^2 + 4x + 7}{6x} ; dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{7}{6} \ln|x| + C $$
More Information
This result shows how to integrate rational functions by simplifying the expression before integrating. Each term can be treated separately, allowing for straightforward integration techniques.
Tips
- Not Simplifying First: Some may forget to simplify the expression before integrating, complicating the process. Always simplify when possible.
- Ignoring the Constant of Integration: It's crucial to remember to include ( C ) after performing indefinite integrals.