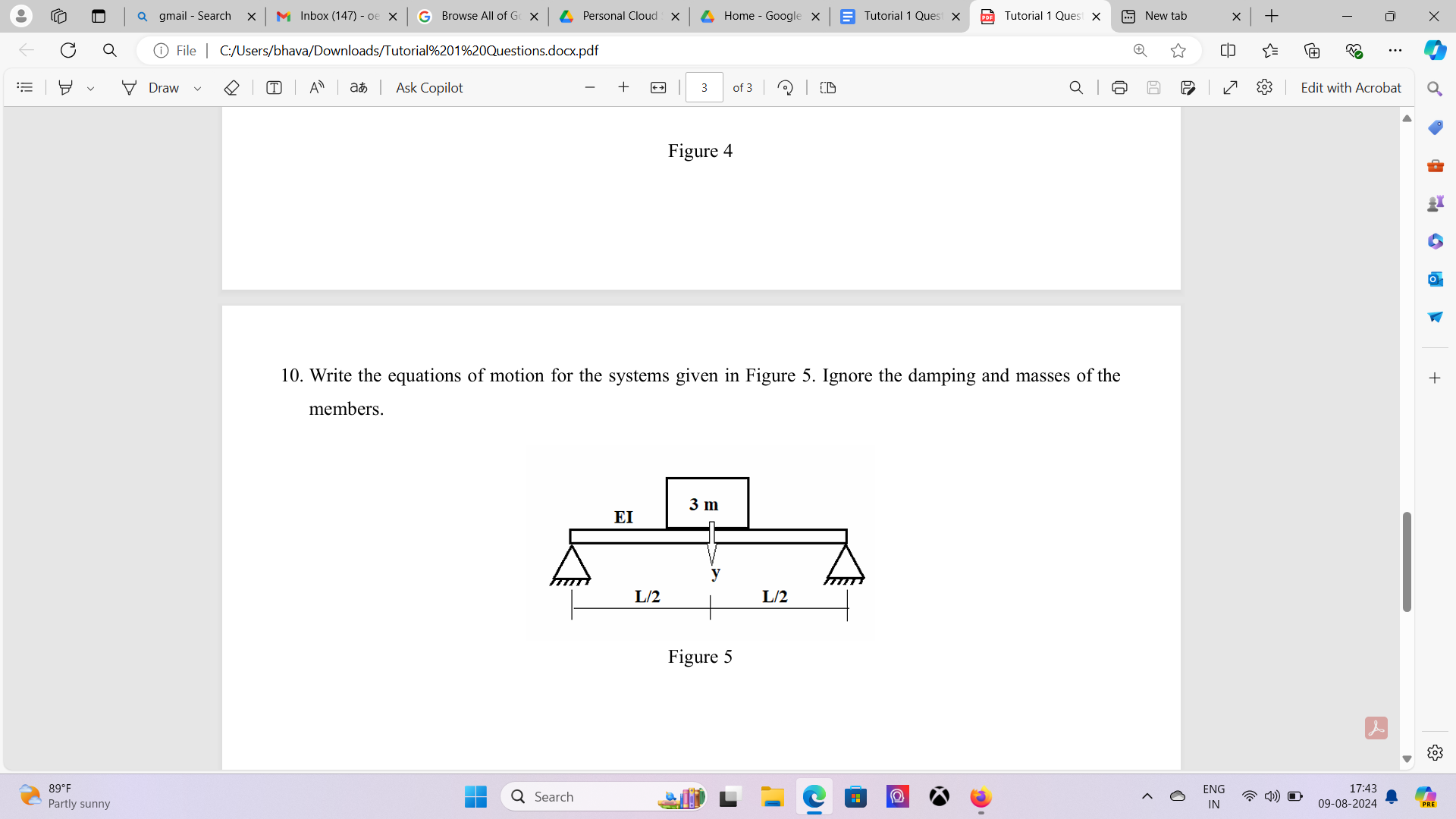
Write the equations of motion for the systems given in Figure 5. Ignore the damping and masses of the members.
Understand the Problem
The question is asking to derive the equations of motion for a given mechanical system depicted in the attached figure. It specifies to ignore the damping effects and the masses of the system members, which suggests a focus on the fundamental equations involved in the dynamics of the structure.
Answer
\( \frac{d^2}{dt^2}(3m) + \frac{6EI}{L^3}y = 0 \)
The equation of motion for the system shown in Figure 5 is: ( \frac{d^2}{dt^2}(3m) + \frac{6EI}{L^3}y = 0 ).
Answer for screen readers
The equation of motion for the system shown in Figure 5 is: ( \frac{d^2}{dt^2}(3m) + \frac{6EI}{L^3}y = 0 ).
More Information
This equation represents a simplified model of the system, ignoring any effects from mass or damping, focusing solely on elasticity.
Tips
A common mistake is failing to recognize that damping and masses are ignored, leading to incorrect application of dynamic equations.
Sources
AI-generated content may contain errors. Please verify critical information