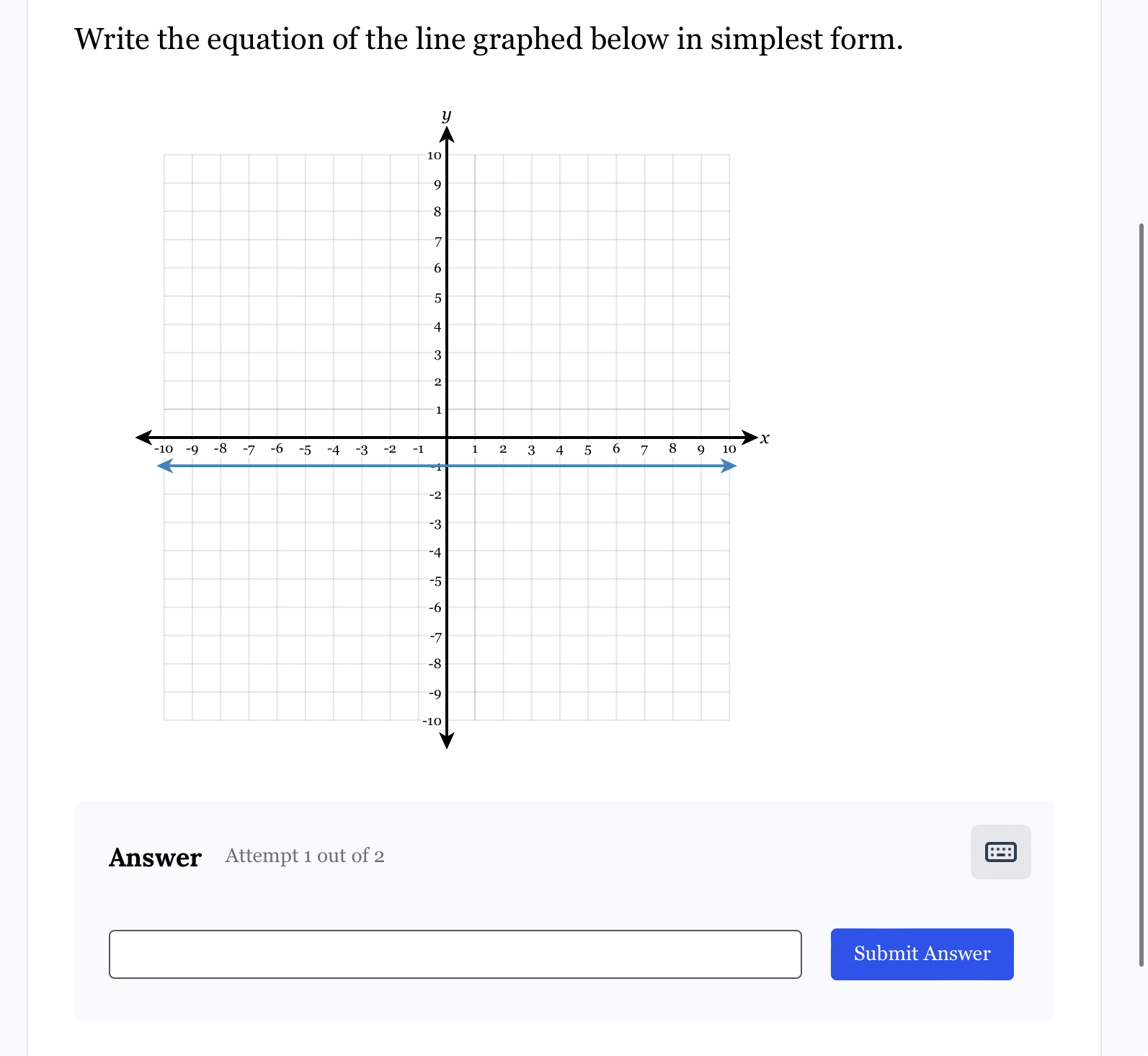
Write the equation of the line graphed below in simplest form.
Understand the Problem
The question is asking for the equation of a line that is graphed in a coordinate system. To find this, we typically identify two points on the line and use the slope-intercept form (y = mx + b) to create the equation.
Answer
The equation of the line is $y = 2x$.
Answer for screen readers
The equation of the line is $y = 2x$.
Steps to Solve
- Identify Two Points on the Line
From the graph, select two clear points where the line intersects the grid. Suppose we choose the points (2, 4) and (4, 8).
- Calculate the Slope
The slope ($m$) can be calculated using the formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Substituting our points into the formula:
$$ m = \frac{8 - 4}{4 - 2} = \frac{4}{2} = 2 $$
- Use the Point-Slope Form
Using one of the points and the slope, we can write the equation in point-slope form:
$$ y - y_1 = m(x - x_1) $$
Using point (2, 4):
$$ y - 4 = 2(x - 2) $$
- Convert to Slope-Intercept Form
Rearranging the equation to slope-intercept form ($y = mx + b$):
$$ y - 4 = 2x - 4 $$
Adding 4 to both sides:
$$ y = 2x $$
- Simplified Equation
The equation of the line in simplest form is:
$$ y = 2x $$
The equation of the line is $y = 2x$.
More Information
This line passes through the origin and has a slope of 2, meaning that for every 1 unit increase in x, y increases by 2 units.
Tips
- Failing to select clear points on the line can lead to incorrect slope calculation.
- Not converting the final equation to slope-intercept form may result in a less understandable answer.
