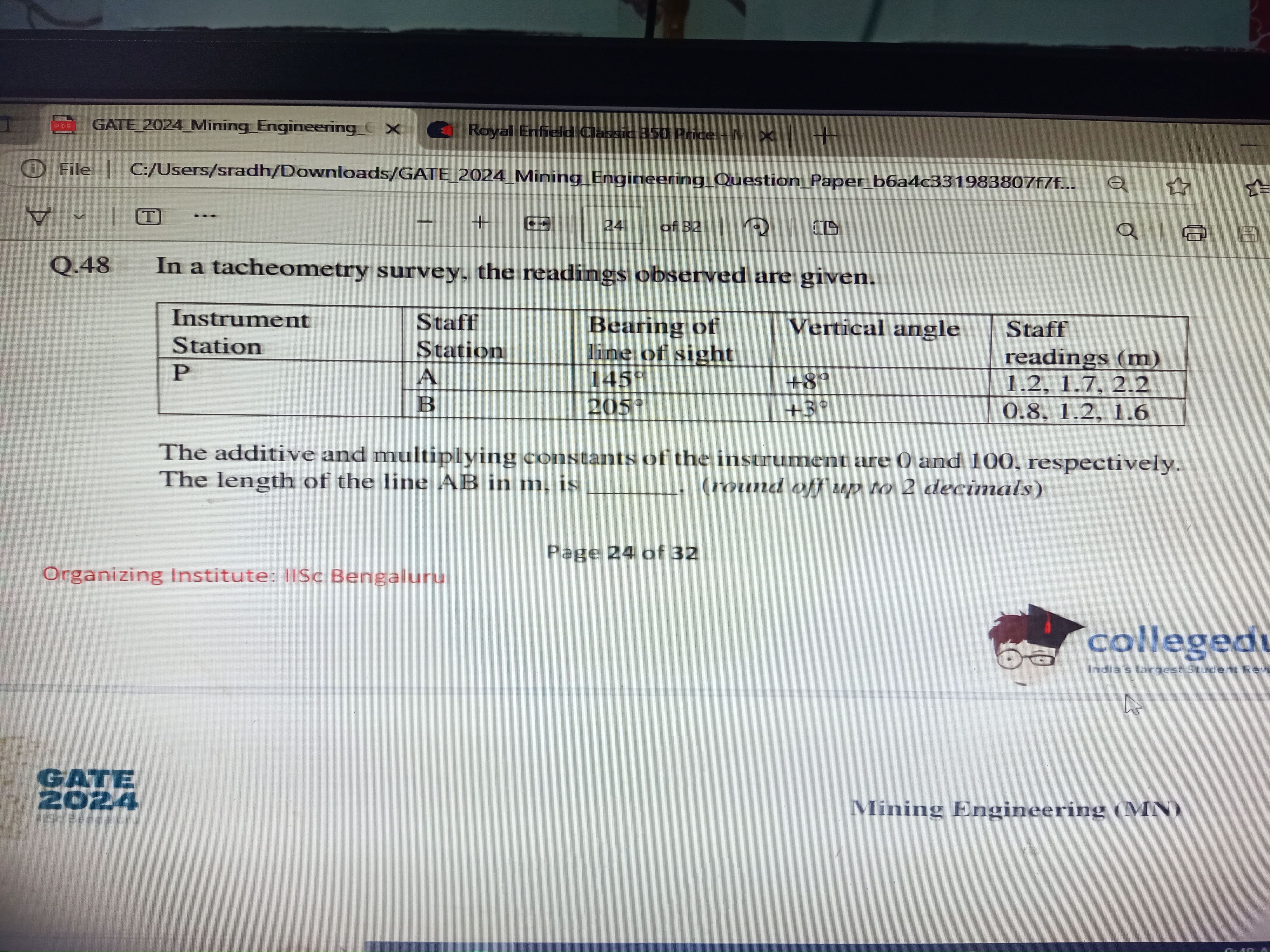
In a tacheometry survey, the readings observed are given. The additive and multiplying constants of the instrument are 0 and 100, respectively. The length of the line AB in m, is (... In a tacheometry survey, the readings observed are given. The additive and multiplying constants of the instrument are 0 and 100, respectively. The length of the line AB in m, is (round off up to 2 decimals). Read more

Steps to Solve

1. Understand the Tacheometry Formula

The tacheometric formula to determine the distance $D$ from the instrument to the staff is given by: $$ D = K \cdot S + C $$ where:

• $K$ is the multiplying constant,
• $S$ is the staff reading,
• $C$ is the additive constant.

2. Identify the Observations

From the provided data:

• The additive constant $C = 0$,
• The multiplying constant $K = 100$,
• Staff readings from station P (A) and B are (1.2, 1.7, 2.2 m) and (0.8, 1.2, 1.6 m), respectively.

3. Calculate the Distances for Each Staff Reading

For each observation, apply the formula:

For Staff A:

• For $S = 1.2$: $$ D_A(1.2) = 100 \cdot 1.2 + 0 = 120 , \text{m} $$
• For $S = 1.7$: $$ D_A(1.7) = 100 \cdot 1.7 + 0 = 170 , \text{m} $$
• For $S = 2.2$: $$ D_A(2.2) = 100 \cdot 2.2 + 0 = 220 , \text{m} $$

For Staff B:

• For $S = 0.8$: $$ D_B(0.8) = 100 \cdot 0.8 + 0 = 80 , \text{m} $$
• For $S = 1.2$: $$ D_B(1.2) = 100 \cdot 1.2 + 0 = 120 , \text{m} $$
• For $S = 1.6$: $$ D_B(1.6) = 100 \cdot 1.6 + 0 = 160 , \text{m} $$

4. Calculate the Average Distance for Each Station

To find the average distances:

• Average distance from station P (A): $$ D_A^{avg} = \frac{120 + 170 + 220}{3} = \frac{510}{3} = 170 , \text{m} $$

• Average distance from station B: $$ D_B^{avg} = \frac{80 + 120 + 160}{3} = \frac{360}{3} = 120 , \text{m} $$

5. Determine the Length of Line AB

The distance between two points A and B can be estimated using the vertical angles. The formula for the horizontal distance is adjusted based on vertical angles, calculated as:

Using the vertical angles:

• Vertical angle from A: $8^\circ$
• Vertical angle from B: $3^\circ$

Using the small angle approximation or trigonometric adjustment, we calculate the effective distance. You can estimate the actual length of line AB using: $$ L_{AB} = \sqrt{D_A^{avg}^2 + D_B^{avg}^2} $$

Compute the effective length more accurately by incorporating the differences in elevation due to vertical angles.