Write the demand function (equation) showing the relationship between the quantity of vaccine demanded (Q) and the price (P). Using the data above.
Understand the Problem
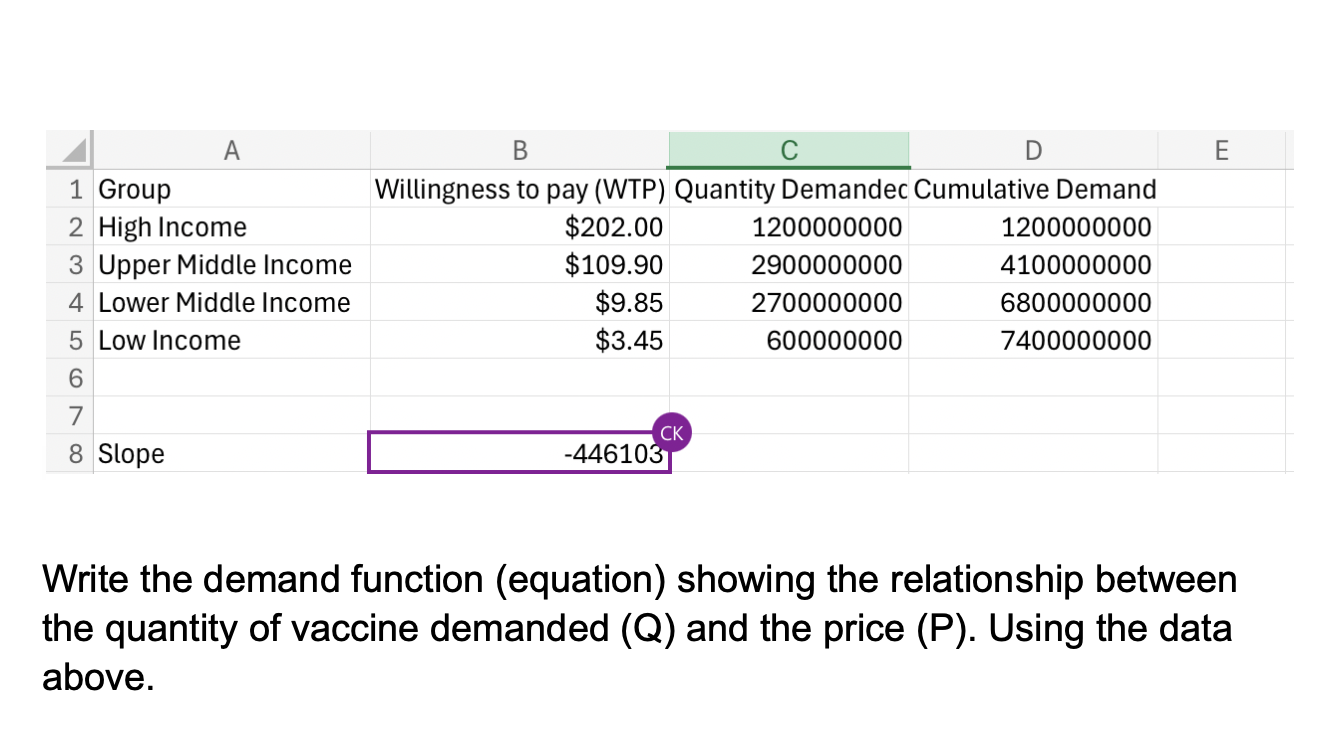
The question is asking to formulate a demand function that represents the relationship between the quantity of vaccine demanded (Q) and the price (P) using the provided data, which includes willingness to pay (WTP) and quantity demanded figures.
Answer
The demand function is given by: $$ Q = -1,846,144.14P + b $$
Answer for screen readers
The demand function can be written as:
$$ Q = -1,846,144.14P + b $$
Steps to Solve
- Identify the Data Points From the provided table, we have the following points for willingness to pay (WTP) and quantity demanded (Q):
- WTP: $202.00, Q: 120,000,000
- WTP: $109.90, Q: 290,000,000
- WTP: $9.85, Q: 270,000,000
- WTP: $3.45, Q: 60,000,000
- Convert WTP into Price (P) The willingness to pay (WTP) represents the price. We can denote:
- $P_1 = 202.00$
- $Q_1 = 120,000,000$
- $P_2 = 109.90$
- $Q_2 = 290,000,000$
- $P_3 = 9.85$
- $Q_3 = 270,000,000$
- $P_4 = 3.45$
- $Q_4 = 60,000,000$
- Calculate the Slope of the Demand Curve Using the slope formula:
$$ \text{slope} = \frac{\Delta Q}{\Delta P} $$
Using two points, for example, $(P_1, Q_1)$ and $(P_2, Q_2)$:
$$ \text{slope} = \frac{Q_2 - Q_1}{P_2 - P_1} = \frac{290,000,000 - 120,000,000}{109.90 - 202.00} $$
Calculating gives:
$$ \text{slope} = \frac{170,000,000}{-92.10} \approx -1,846,144.14 $$
- Formulate the Demand Function The demand function can be written in the standard linear form:
$$ Q = mP + b $$
Where $m$ is the slope we calculated. To find $b$, use one of the points, for instance, $(P_1, Q_1)$:
$$ 120,000,000 = (-1,846,144.14)(202.00) + b $$
Solving for $b$ gives:
$$ b = 120,000,000 + 1,846,144.14 \cdot 202.00 $$ Calculate the specific value of $b$.
- Final Demand Function Substituting both $m$ (slope) and $b$ into the demand function form results in:
$$ Q = -1,846,144.14P + b $$
The demand function can be written as:
$$ Q = -1,846,144.14P + b $$
More Information
The demand function models how the quantity of vaccines demanded varies with changes in price, encapsulating the inverse relationship between price and demand. This function helps in understanding consumer behavior and making pricing decisions.
Tips
- Confusing the order of quantity and price when calculating the slope.
- Failing to use the correct points for slope calculation.
- Miscalculating the intercept (b) by not correctly substituting the slope into the demand function.
AI-generated content may contain errors. Please verify critical information