Write an inequality that represents the graph.
Understand the Problem
The question asks for an inequality that corresponds to a given graph. This graph likely depicts a linear inequality, which can be found by determining the line's slope and y-intercept, as well as the direction of the shading to indicate whether it is a 'greater than' or 'less than' relationship.
Answer
The inequality is \(y > x\).
Answer for screen readers
The inequality is (y > x).
Steps to Solve
-
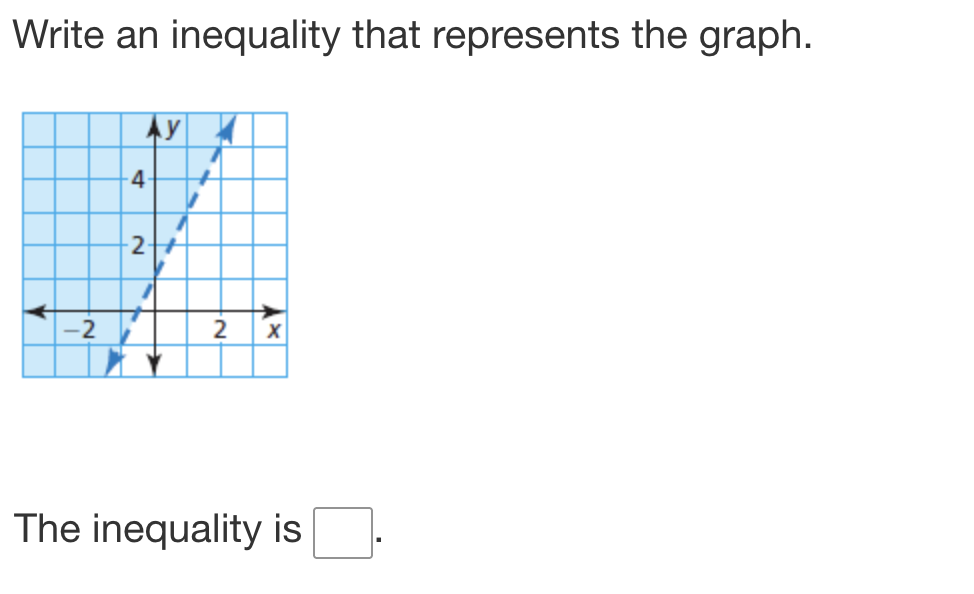
Identify the line from the graph
The given graph shows a dashed line. This indicates that the inequality does not include the line itself (i.e., "greater than" or "less than" without "equal to"). -
Determine the slope and y-intercept
From the graph, we see that the line passes through the points ((-2, 0)) and ((2, 4)). To find the slope (m), use the formula: $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{4 - 0}{2 - (-2)} = \frac{4}{4} = 1 $$ The slope is 1. The y-intercept (b) is 0, since it crosses the y-axis at (y = 0). -
Write the equation of the line
The equation of the line in slope-intercept form is: $$ y = mx + b \implies y = 1x + 0 \implies y = x $$ -
Determine the direction of the inequality
The graph has shading above the line (y = x), indicating that the inequality represents all points where (y) is greater than (x). -
Write the final inequality
Considering the dashed line and the shading, the inequality is: $$ y > x $$
The inequality is (y > x).
More Information
This inequality indicates that all points above the line (y = x) are included, but the line itself is not part of the solution. Dashed lines in graphs signify that the boundary is not included in the solution set.
Tips
- Ignoring the type of line: Sometimes students confuse solid and dashed lines. Remember, a dashed line means "greater than" or "less than" (not equal), while a solid line means "greater than or equal to" or "less than or equal to."
- Misinterpreting the shading: Always ensure you correctly interpret which side of the line is shaded and adjust the inequality direction accordingly.
AI-generated content may contain errors. Please verify critical information