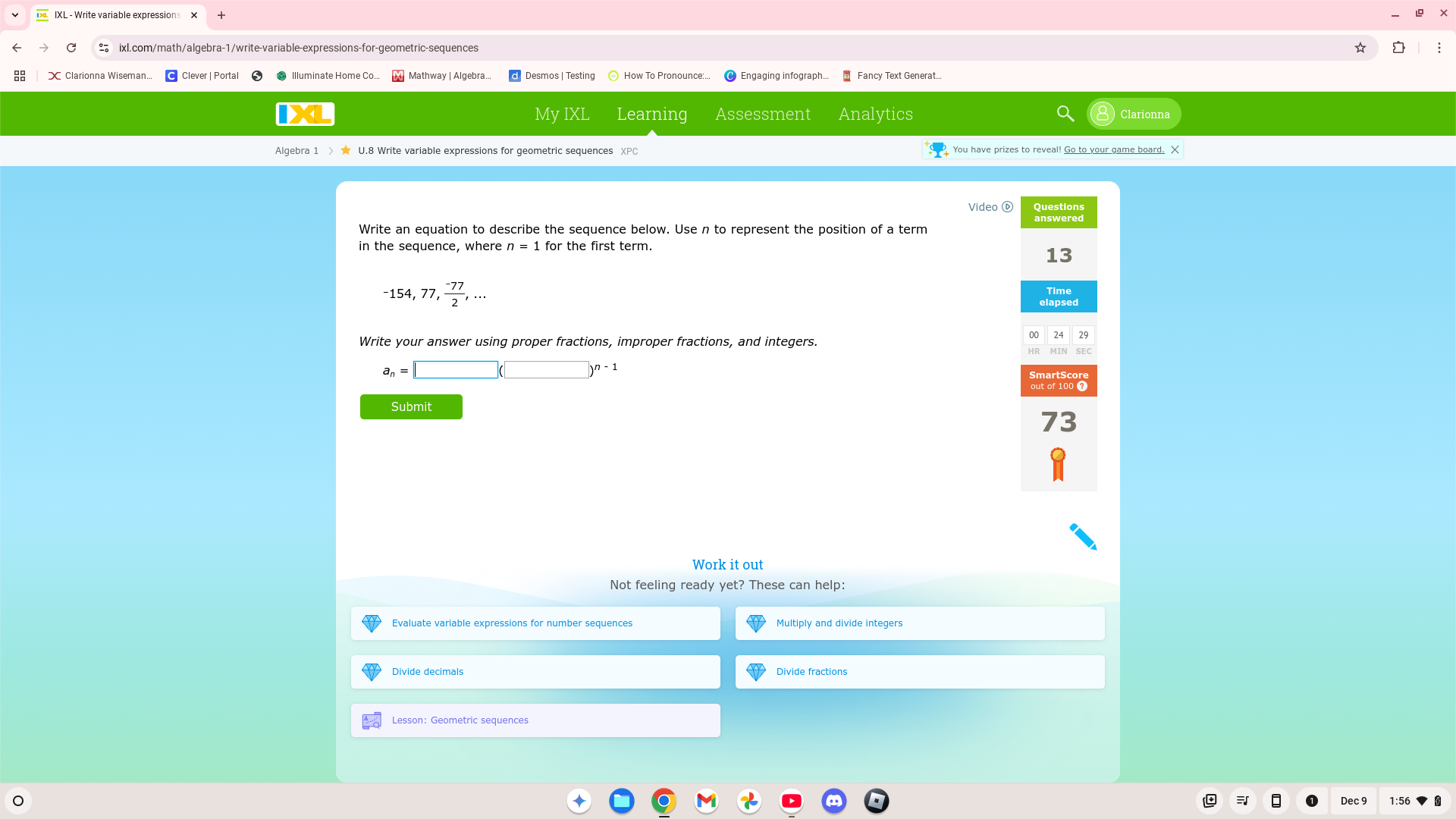
Write an equation to describe the sequence below, where n = 1 for the first term: -154, 77, -\frac{77}{2}, ...
Understand the Problem
The question is asking for an equation that describes a given geometric sequence, where 'n' represents the position of each term in the sequence. The user must determine the pattern from the provided terms and construct a formula for the n-th term.
Answer
The n-th term of the geometric sequence is given by: $$ a_n = -154 \cdot \left(-\frac{1}{2}\right)^{n-1} $$
Answer for screen readers
The equation for the n-th term of the sequence is:
$$ a_n = -154 \cdot \left(-\frac{1}{2}\right)^{n-1} $$
Steps to Solve
- Identify the geometric sequence pattern
The given terms are:
- First term ($a_1$): $-154$
- Second term ($a_2$): $77$
- Third term ($a_3$): $-\frac{77}{2}$
We need to find the common ratio ($r$) between consecutive terms.
- Calculate the common ratio
To find the common ratio, divide the second term by the first term:
$$ r = \frac{a_2}{a_1} = \frac{77}{-154} = -\frac{1}{2} $$
Now, calculate the ratio between the third term and the second term:
$$ r = \frac{a_3}{a_2} = \frac{-\frac{77}{2}}{77} = -\frac{1}{2} $$
So, the common ratio is consistent.
- Generalize the formula for the n-th term
The formula for a geometric sequence is:
$$ a_n = a_1 \cdot r^{n-1} $$
Substituting in the values for $a_1$ and $r$:
$$ a_n = -154 \cdot \left(-\frac{1}{2}\right)^{n-1} $$
- Write the final expression
Thus, the equation to describe the sequence is:
$$ a_n = -154 \cdot \left(-\frac{1}{2}\right)^{n-1} $$
The equation for the n-th term of the sequence is:
$$ a_n = -154 \cdot \left(-\frac{1}{2}\right)^{n-1} $$
More Information
This formula allows you to find any term in the geometric sequence by substituting a value for $n$. The pattern shows that the sequence alternates signs due to the negative base, and the magnitudes decrease by half with each term.
Tips
- Not checking the common ratio: It's crucial to verify that the ratio remains consistent for all terms.
- Forgetting to adjust the exponent: The exponent for the common ratio should start at $n-1$ for the first term.
AI-generated content may contain errors. Please verify critical information