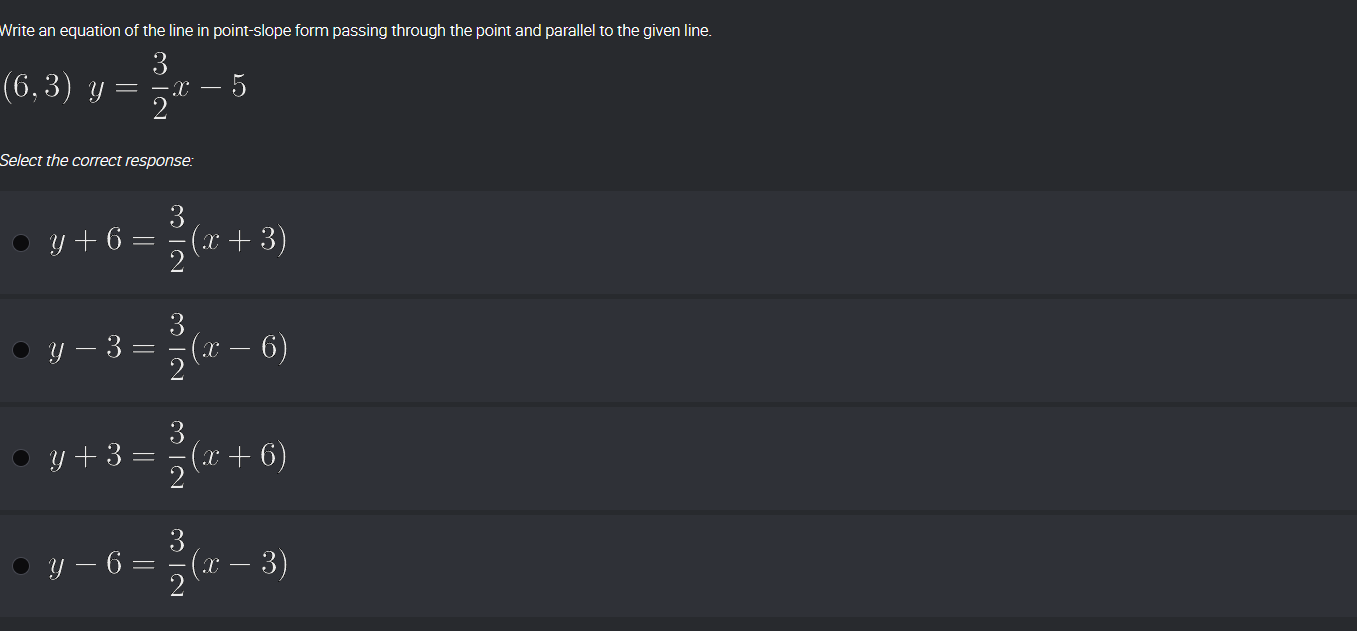
Write an equation of the line in point-slope form passing through the point (6, 3) and parallel to the given line y = \frac{3}{2}x - 5.
Understand the Problem
The question is asking for the equation of a line in point-slope form that is parallel to a given line and passes through a specified point. The slope of the given line is rac{3}{2}, and we need to use this slope along with the point (6, 3) to write the equation.
Answer
The equation is $y - 3 = \frac{3}{2}(x - 6)$.
Answer for screen readers
The equation of the line in point-slope form is: $$ y - 3 = \frac{3}{2}(x - 6) $$
Steps to Solve
- Identify the slope and the point to use
The slope of the given line is $m = \frac{3}{2}$. The point through which the new line must pass is $(6, 3)$.
- Use the point-slope form of the equation
The point-slope form is given by the formula: $$ y - y_1 = m(x - x_1) $$
Substituting in the values for the slope and the point $(x_1, y_1) = (6, 3)$: $$ y - 3 = \frac{3}{2}(x - 6) $$
- Rearrange the equation if needed
To express it in a standard form: $$ y - 3 = \frac{3}{2}(x - 6) $$
This can be left as the answer or simplified further if necessary.
The equation of the line in point-slope form is: $$ y - 3 = \frac{3}{2}(x - 6) $$
More Information
This equation represents a line that is parallel to the original line with a slope of $\frac{3}{2}$ and passes through the point $(6, 3)$. The point-slope form is particularly useful for quickly writing equations of lines when you know a point and slope.
Tips
- Forgetting to use the given point: Always ensure you substitute the correct coordinates of the point into the equation.
- Mixing up the addition/subtraction in the point-slope formula: Remember, it's $y - y_1$ and $x - x_1$, not vice versa.
AI-generated content may contain errors. Please verify critical information