Write an equation of the line in point-slope form passing through the point (-4, 1) and parallel to the given line y = -2x + 3.
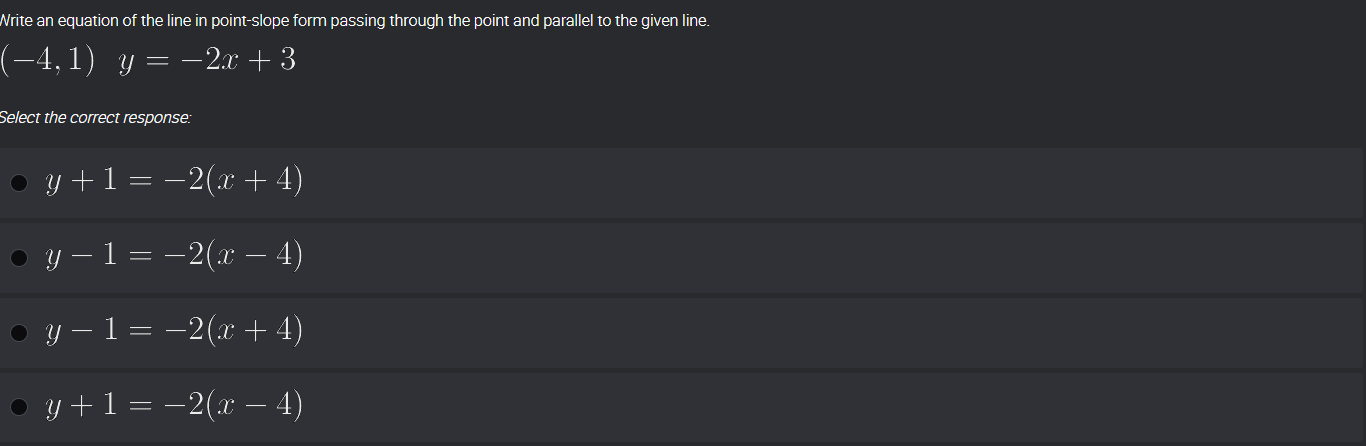
Understand the Problem
The question is asking to write the equation of a line in point-slope form that passes through a specific point and is parallel to a given line. The given line is presented in slope-intercept form, from which the slope can be extracted to use for constructing the equation of the new line.
Answer
$$ y + 1 = -2(x + 4) $$
Answer for screen readers
The equation of the line in point-slope form is:
$$ y + 1 = -2(x + 4) $$
Steps to Solve
- Identify the slope of the given line
The given line is in the slope-intercept form $y = -2x + 3$. Therefore, the slope $m$ is $-2$.
- Use the point-slope form equation
The point-slope form is given by the formula:
$$ y - y_1 = m(x - x_1) $$
where $(x_1, y_1)$ is the point through which the line passes. Here, $(x_1, y_1) = (-4, 1)$ and $m = -2$.
- Substitute values into the equation
Substituting the values into the point-slope form equation:
$$ y - 1 = -2(x - (-4)) $$
This simplifies to:
$$ y - 1 = -2(x + 4) $$
- Adjust the equation (if needed)
We can rearrange the equation:
$$ y + 1 = -2(x + 4) $$
This matches the point-slope form as requested.
The equation of the line in point-slope form is:
$$ y + 1 = -2(x + 4) $$
More Information
The point-slope form of a line is particularly useful when you know a point on the line and its slope. Because parallel lines have the same slope, we used the slope from the given line to create the new equation.
Tips
- Forgetting to maintain the sign of the slope can lead to an incorrect equation.
- Mixing up the coordinates when substituting values can lead to a wrong point-slope equation.
AI-generated content may contain errors. Please verify critical information