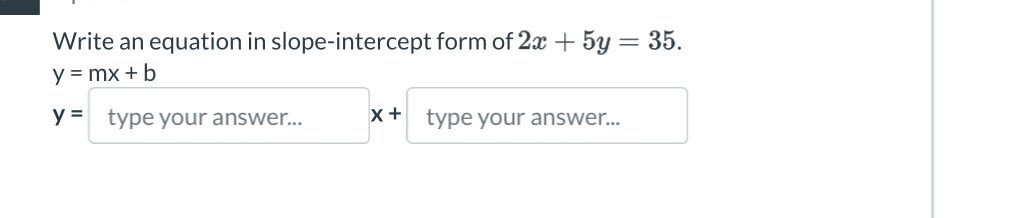
Write an equation in slope-intercept form of 2x + 5y = 35.
Understand the Problem
The question is asking us to convert the given equation, 2x + 5y = 35, into the slope-intercept form (y = mx + b). This involves isolating y on one side of the equation.
Answer
The equation in slope-intercept form is \( y = -\frac{2}{5}x + 7 \).
Answer for screen readers
The equation in slope-intercept form is ( y = -\frac{2}{5}x + 7 ).
Steps to Solve
- Isolate the term with y
Start with the original equation: $$ 2x + 5y = 35 $$
Subtract $2x$ from both sides to isolate the term with $y$: $$ 5y = 35 - 2x $$
- Divide by the coefficient of y
Now, divide every term by 5 to solve for $y$: $$ y = \frac{35}{5} - \frac{2x}{5} $$
- Simplify the expression
Calculate the division: $$ y = 7 - \frac{2}{5}x $$
- Rewrite in slope-intercept form
Rearranging the equation gives: $$ y = -\frac{2}{5}x + 7 $$
The equation in slope-intercept form is ( y = -\frac{2}{5}x + 7 ).
More Information
In the slope-intercept form ( y = mx + b ), ( m ) represents the slope of the line and ( b ) represents the y-intercept. Here, the slope is ( -\frac{2}{5} ), which indicates that for every 5 units you move to the right along the x-axis, the line moves down 2 units. The y-intercept is 7, which means the line crosses the y-axis at ( (0, 7) ).
Tips
- Forgetting to isolate $y$ before dividing by the coefficient can lead to errors.
- Not simplifying fractions can result in a less clear answer.
- Mixing up the signs while rearranging the equation.
AI-generated content may contain errors. Please verify critical information