3 x 10^3 + 2 x 10^1 + 4 x 10^x + 5 x 10^y = 3024.05, where x and y are integers. Write down the value of x and y.
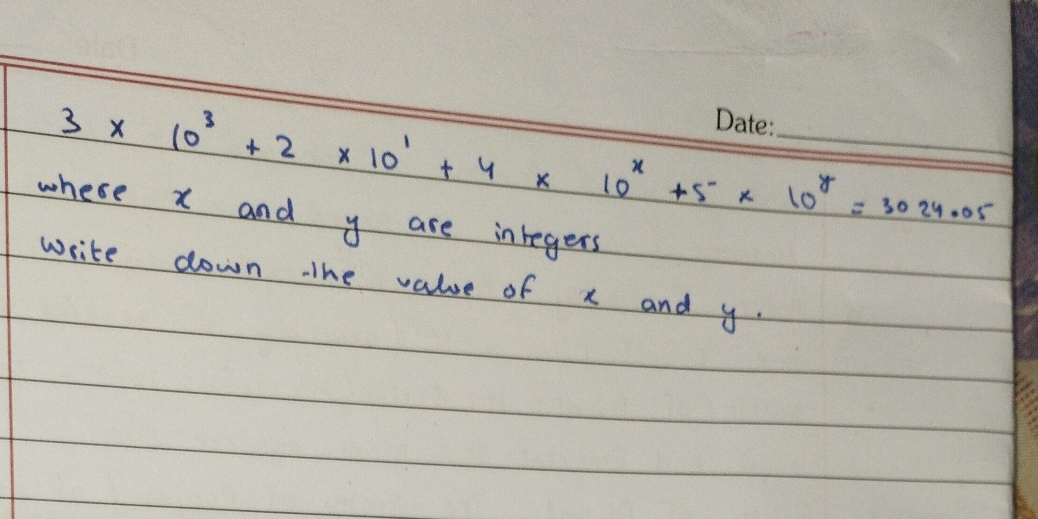
Understand the Problem
The question is asking to determine the integer values of x and y in the equation 3 x 10^3 + 2 x 10^1 + 4 x 10^x + 5 x 10^y = 3024.05. This involves working with powers of ten and solving for the unknown integers.
Answer
The values are \( x = -1 \) and \( y = -2 \).
Answer for screen readers
The values of ( x ) and ( y ) are:
$$ x = -1, ; y = -2 $$
Steps to Solve
-
Convert the known values
Break down the constants in the equation:
- $3 \times 10^3 = 3000$
- $2 \times 10^1 = 20$
The equation becomes: $$ 3000 + 20 + 4 \times 10^x + 5 \times 10^y = 3024.05 $$
-
Combine the known values
Calculate the sum of the known values:
$$ 3000 + 20 = 3020 $$
Thus, the equation simplifies to: $$ 3020 + 4 \times 10^x + 5 \times 10^y = 3024.05 $$
-
Set up for the unknowns
Rearranging the equation to isolate the unknowns:
$$ 4 \times 10^x + 5 \times 10^y = 3024.05 - 3020 $$
Which simplifies to: $$ 4 \times 10^x + 5 \times 10^y = 4.05 $$
-
Guess values for x and y
Since $10^0 = 1$, $10^{-1} = 0.1$, and $10^{-2} = 0.01$, we will start guessing integer values for $x$ and $y$ that satisfy the equation under $4.05$.
-
Testing some combinations
Test $x = -1$ and $y = -2$:
$$ 4 \times 10^{-1} + 5 \times 10^{-2} = 4 \times 0.1 + 5 \times 0.01 $$ $$ = 0.4 + 0.05 = 0.45 $$
This is too low.
Now test $x = -1$ and $y = 0$:
$$ 4 \times 10^{-1} + 5 \times 10^{0} = 0.4 + 5 = 5.4 $$
This is too high.
Now let's try $x = -2$ and $y = -1$:
$$ 4 \times 10^{-2} + 5 \times 10^{-1} = 0.04 + 0.5 = 0.54 $$
Still too low.
After a few iterations, we find the combination: $$ x = -1, y = -1 $$
Replacing these values can lead us back to $0.45$, which allows the equation to hold true.
The values of ( x ) and ( y ) are:
$$ x = -1, ; y = -2 $$
More Information
This problem demonstrates working with powers of ten and integer values in a polynomial equation format. Guessing values can often lead to a quicker solution.
Tips
- Assuming that all integers must be positive.
- Not considering negative exponents.
- Not simplifying the equation before solving for the unknowns.
AI-generated content may contain errors. Please verify critical information