Which values from the set satisfy this inequality: -10 - 2x > 30? Select TWO correct answers from the set {-30, -25, 20, 0, 20, 25, 30}.

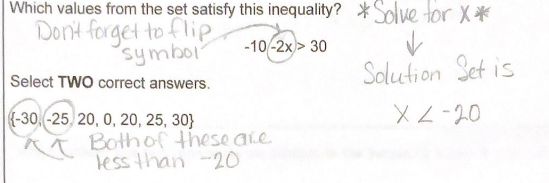
Understand the Problem

The question is asking to identify which values from a given set satisfy the inequality -10 - 2x > 30. It requires solving the inequality for x and selecting the correct values from the provided options.

Answer

The values are $-30$ and $-25$.

Steps to Solve

Isolate the variable x

Start by isolating $x$ in the inequality $-10 - 2x > 30$.

Add 10 to both sides of the inequality:

$$ -2x > 30 + 10 $$

This simplifies to:

$$ -2x > 40 $$

Divide by -2 and flip the inequality

Next, divide both sides by -2. Remember that when dividing or multiplying by a negative number, the direction of the inequality sign changes:

$$ x < \frac{40}{-2} $$

This simplifies to:

$$ x < -20 $$

Identify the solution set

Now that we have the solution $x < -20$, we need to identify the values from the provided set that meet this condition.

The values provided are: $$ {-30, -25, 20, 0, 20, 25, 30} $$

Select the appropriate values

Review each value to find which ones are less than -20:

$-30 < -20$ (satisfies the inequality)
$-25 < -20$ (satisfies the inequality)
$20 > -20$ (does not satisfy)
$0 > -20$ (does not satisfy)
$20 > -20$ (does not satisfy)
$25 > -20$ (does not satisfy)
$30 > -20$ (does not satisfy)

Thus, the correct values are $-30$ and $-25$.

The correct answers are $-30$ and $-25$.

More Information

The solution established that both $-30$ and $-25$ satisfy the inequality $-10 - 2x > 30$, confirming that they are both less than $-20$.

Tips

Forgetting to flip the inequality sign when dividing by a negative number. Always remember to reverse the direction of the inequality when this occurs.
Misinterpreting the solution set; ensure to double-check all values against the inequality.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!