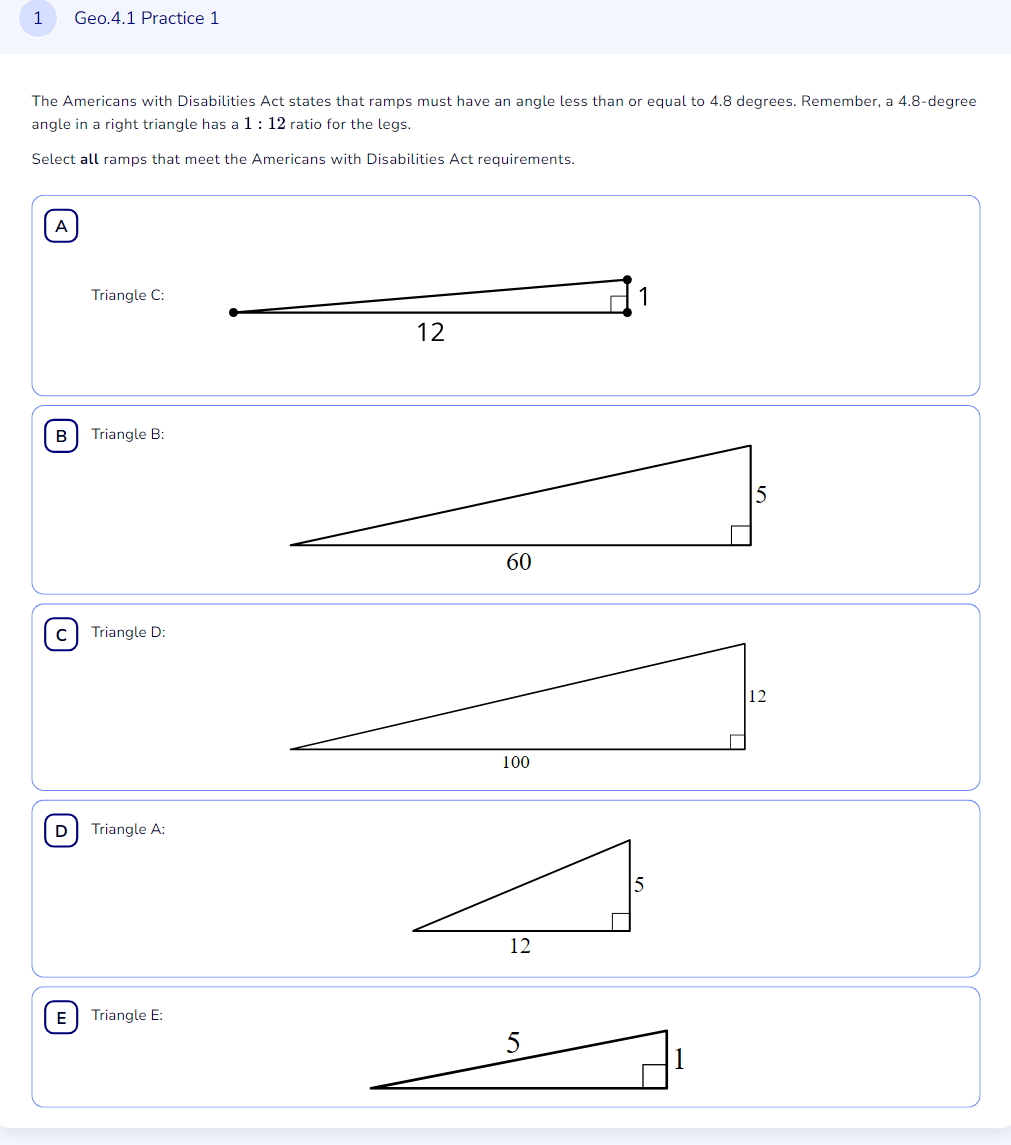
Which triangles meet the Americans with Disabilities Act requirements for ramps with an angle less than or equal to 4.8 degrees and a 1:12 ratio for the legs?

Steps to Solve

1. Identify the ratio for compliance

The Americans with Disabilities Act specifies a 1:12 ratio, which indicates that for every unit of height (rise), there should be 12 units of length (run) in a right triangle. This can be interpreted as:

$$ \text{rise} = \frac{1}{12} \times \text{run} $$

2. Determine the angles for each triangle

You can find the angle of elevation (let's call it $\theta$) for each triangle using the tangent function:

$$ \tan(\theta) = \frac{\text{rise}}{\text{run}} $$

The angle $\theta$ can then be calculated as:

$$ \theta = \tan^{-1}\left(\frac{\text{rise}}{\text{run}}\right) $$

3. Calculate angles for the given triangles

• Triangle C: Rise = 1, Run = 12 $$ \theta = \tan^{-1}\left(\frac{1}{12}\right) $$

• Triangle B: Rise = 5, Run = 60 $$ \theta = \tan^{-1}\left(\frac{5}{60}\right) $$

• Triangle D: Rise = 12, Run = 100 $$ \theta = \tan^{-1}\left(\frac{12}{100}\right) $$

• Triangle A: Rise = 5, Run = 12 $$ \theta = \tan^{-1}\left(\frac{5}{12}\right) $$

• Triangle E: Rise = 1, Run = 5 $$ \theta = \tan^{-1}\left(\frac{1}{5}\right) $$

4. Evaluate each angle

Now, use a calculator for each calculation to evaluate which angles are less than or equal to 4.8 degrees.

5. Select compliant triangles

After calculating, compare each angle to 4.8 degrees to determine which triangles meet the compliance requirement.