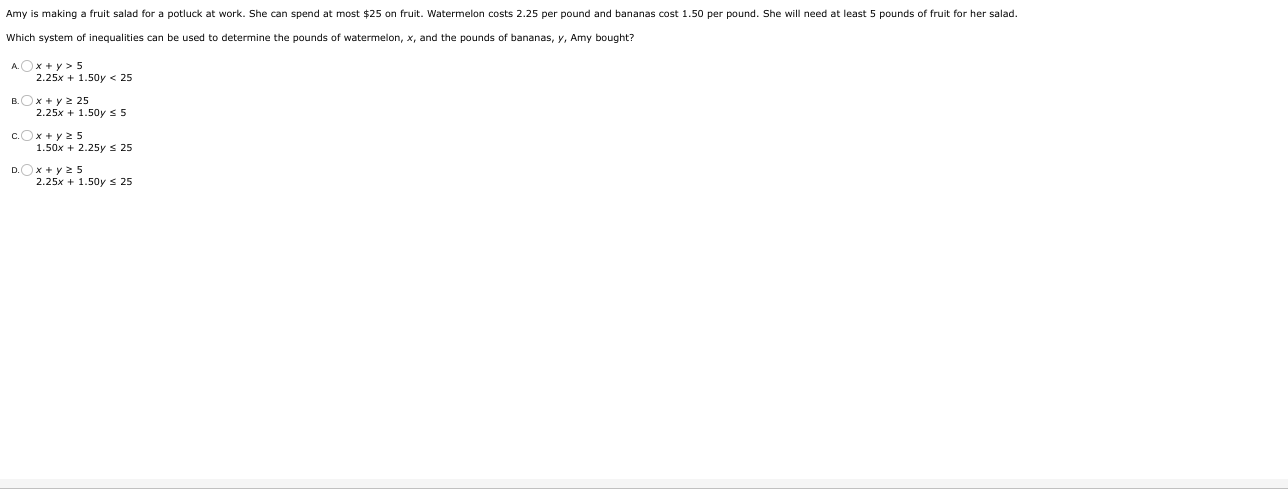
Which system of inequalities can be used to determine the pounds of watermelon, x, and the pounds of bananas, y, Amy bought?
Understand the Problem
The question is asking to identify the correct system of inequalities that represents Amy's budget and fruit requirements for her fruit salad. It involves cost limitations and minimum weight constraints.
Answer
$$ x + y \geq 5; \quad 2.25x + 1.50y \leq 25 $$
Answer for screen readers
The correct system of inequalities is: $$ x + y \geq 5 $$ $$ 2.25x + 1.50y \leq 25 $$
Steps to Solve
-
Understanding Costs Amy can spend up to $25 on fruit. The cost per pound of watermelon ($x$) is $2.25, and the cost per pound of bananas ($y$) is $1.50. The relationship for cost is: $$ 2.25x + 1.50y \leq 25 $$
-
Minimum Weight Requirement Amy needs at least 5 pounds of fruit. This gives us the inequality: $$ x + y \geq 5 $$
-
Upper Bound for Total Weight Since there is a cap on the total fruit she can buy, we set it: $$ x + y \leq 25 $$
-
Combining Inequalities Now we combine the inequalities based on the constraints:
-
Cost: $$ 2.25x + 1.50y \leq 25 $$
-
Minimum weight: $$ x + y \geq 5 $$
-
Upper Bound weight: $$ x + y \leq 25 $$
The correct system of inequalities is: $$ x + y \geq 5 $$ $$ 2.25x + 1.50y \leq 25 $$
More Information
This system captures Amy's budget and fruit weight requirements. The first inequality enforces the minimum fruit weight, while the second keeps her spending within budget.
Tips
- Confusing the direction of the inequalities (greater than vs. less than).
- Failing to account for both the minimum weight and the cost constraints.
AI-generated content may contain errors. Please verify critical information