Which statement is true about the solution to the system of equations? A. The system has no solutions. B. The system has exactly one solution. C. The system has exactly two solutio... Which statement is true about the solution to the system of equations? A. The system has no solutions. B. The system has exactly one solution. C. The system has exactly two solutions. D. The system has infinitely many solutions.
Understand the Problem
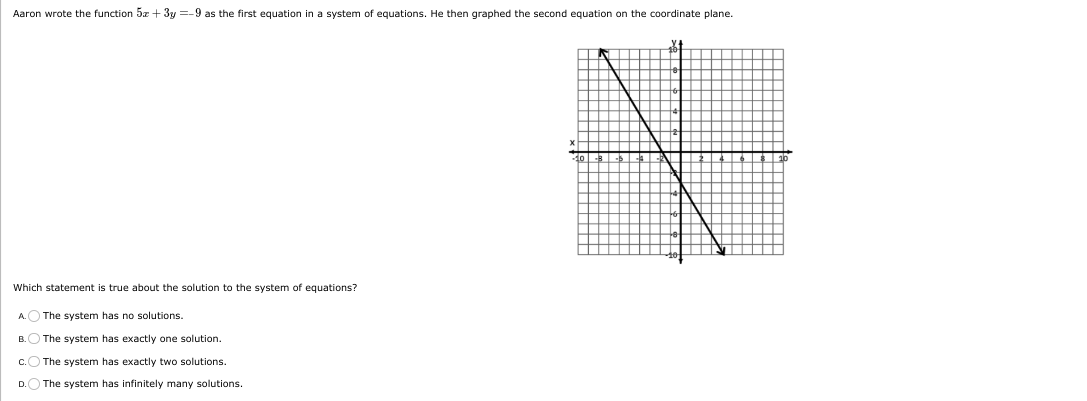
The question is asking which statement is true about the solution to a given system of equations based on the graph provided. The graph shows how the lines intersect, which will help determine whether there are no solutions, one solution, two solutions, or infinitely many solutions.
Answer
The system has exactly one solution.
Answer for screen readers
The system has exactly one solution.
Steps to Solve
-
Identify the Equations from the Graph The first equation given is $5x + 3y = 9$. The second equation can be derived from observing the graph. The line appears to have a negative slope and can be expressed as $y = mx + b$.
-
Convert the First Equation to Slope-Intercept Form To better understand the intersection, convert the first equation to slope-intercept form ($y = mx + b$): $$ 3y = -5x + 9 $$ $$ y = -\frac{5}{3}x + 3 $$ The slope is $-\frac{5}{3}$ and the y-intercept is $3$.
-
Analyze the Graph's Line The line shown in the graph seems to start at y-axis value $4$ when $x = 0$. It is downward sloping and intersects the $x$-axis at approximately $-2$.
-
Determine the Interaction of the Two Lines Since the two lines have different slopes ($-\frac{5}{3}$ for the first equation versus the slope of the second line), they will intersect at one point.
-
Conclusion on the System of Equations Since there is an intersection in the graph, it means the system has exactly one solution.
The system has exactly one solution.
More Information
In a system of linear equations, if two lines intersect, the system has one unique solution where the lines cross. If the lines are parallel, the system has no solutions. If the lines are identical, there are infinitely many solutions.
Tips
- Confusing parallel lines for intersecting lines, leading to the incorrect conclusion of no solutions.
- Miscalculating the slopes, which could suggest multiple solutions.
AI-generated content may contain errors. Please verify critical information