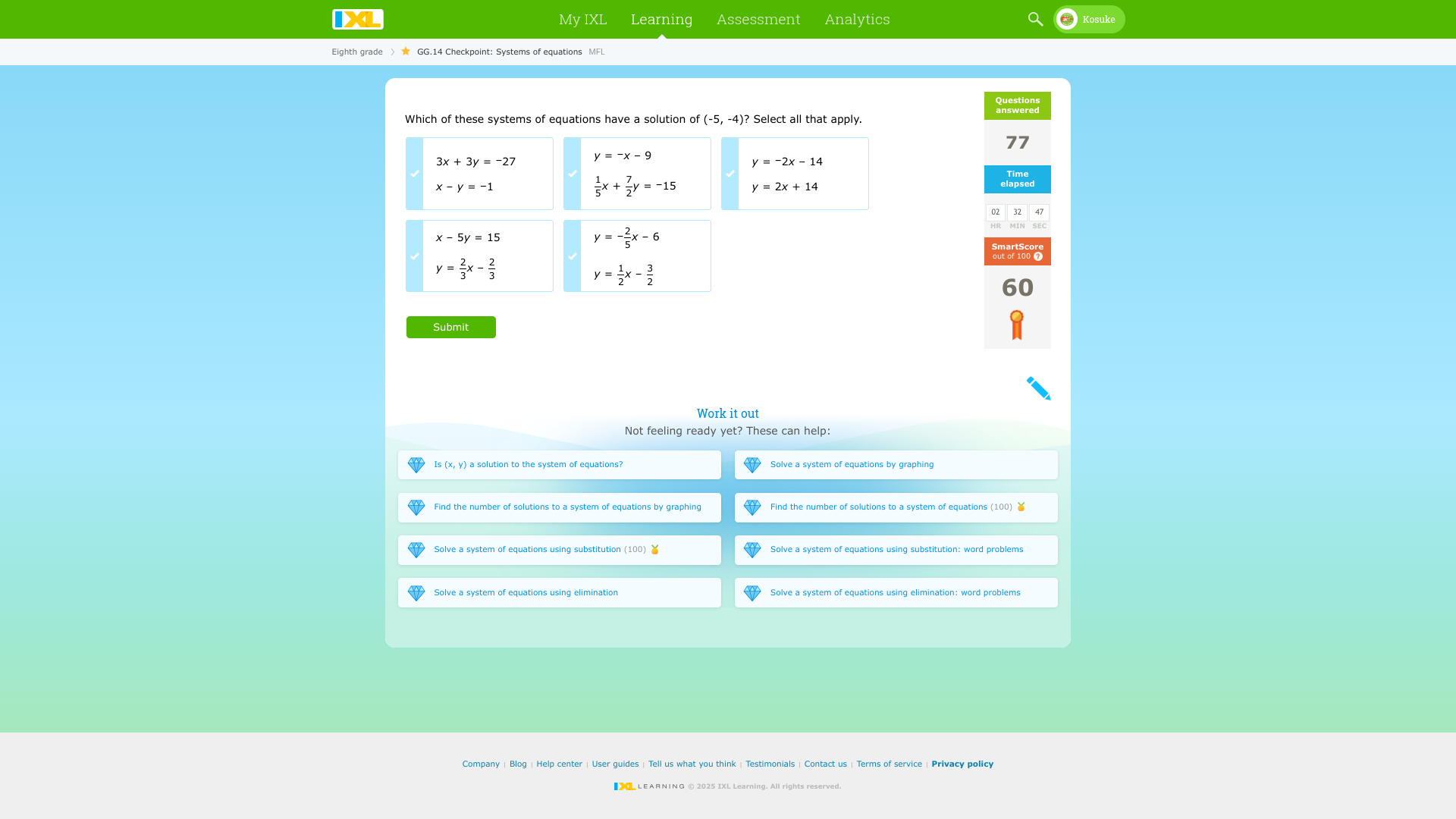
Which of these systems of equations have a solution of (-5, -4)? Select all that apply.

Steps to Solve

1. Substituting the solution into the equations

   For each system of equations, substitute $x = -5$ and $y = -4$ to check if both equations hold true.

2. Check the first system:

   The first system is: $$ 3x + 3y = -27 $$ $$ x - y = -1 $$

   Substituting:

   • For the first equation: $$ 3(-5) + 3(-4) = -15 - 12 = -27 $$ (True)
   • For the second equation: $$ -5 - (-4) = -5 + 4 = -1 $$ (True)

3. Check the second system:

   The second system is: $$ x - 5y = 15 $$

   Substituting:

   • For this equation: $$ -5 - 5(-4) = -5 + 20 = 15 $$ (True)

4. Check the third system:

   The third system is: $$ y = -x - 9 $$

   Substituting:

   • For this equation: $$ -4 = -(-5) - 9 $$ $$ -4 = 5 - 9 = -4 $$ (True)

5. Check the fourth system:

   The fourth system is: $$ y = -\frac{2}{3}x - \frac{2}{3} $$

   Substituting:

   • For this equation: $$ -4 = -\frac{2}{3}(-5) - \frac{2}{3} $$ $$ -4 = \frac{10}{3} - \frac{2}{3} = \frac{8}{3} $$ (False)

6. Check the fifth system:

   The fifth system is: $$ y = -\frac{2}{5}x - 6 $$

   Substituting:

   • For this equation: $$ -4 = -\frac{2}{5}(-5) - 6 $$ $$ -4 = 2 - 6 = -4 $$ (True)

7. Check the sixth system:

   The sixth system is: $$ y = \frac{1}{2}x - \frac{3}{2} $$

   Substituting:

   • For this equation: $$ -4 = \frac{1}{2}(-5) - \frac{3}{2} $$ $$ -4 = -\frac{5}{2} - \frac{3}{2} = -4 $$ (True)