Find the pedal equation of the ellipse x²/4 + y²/36 = 1.
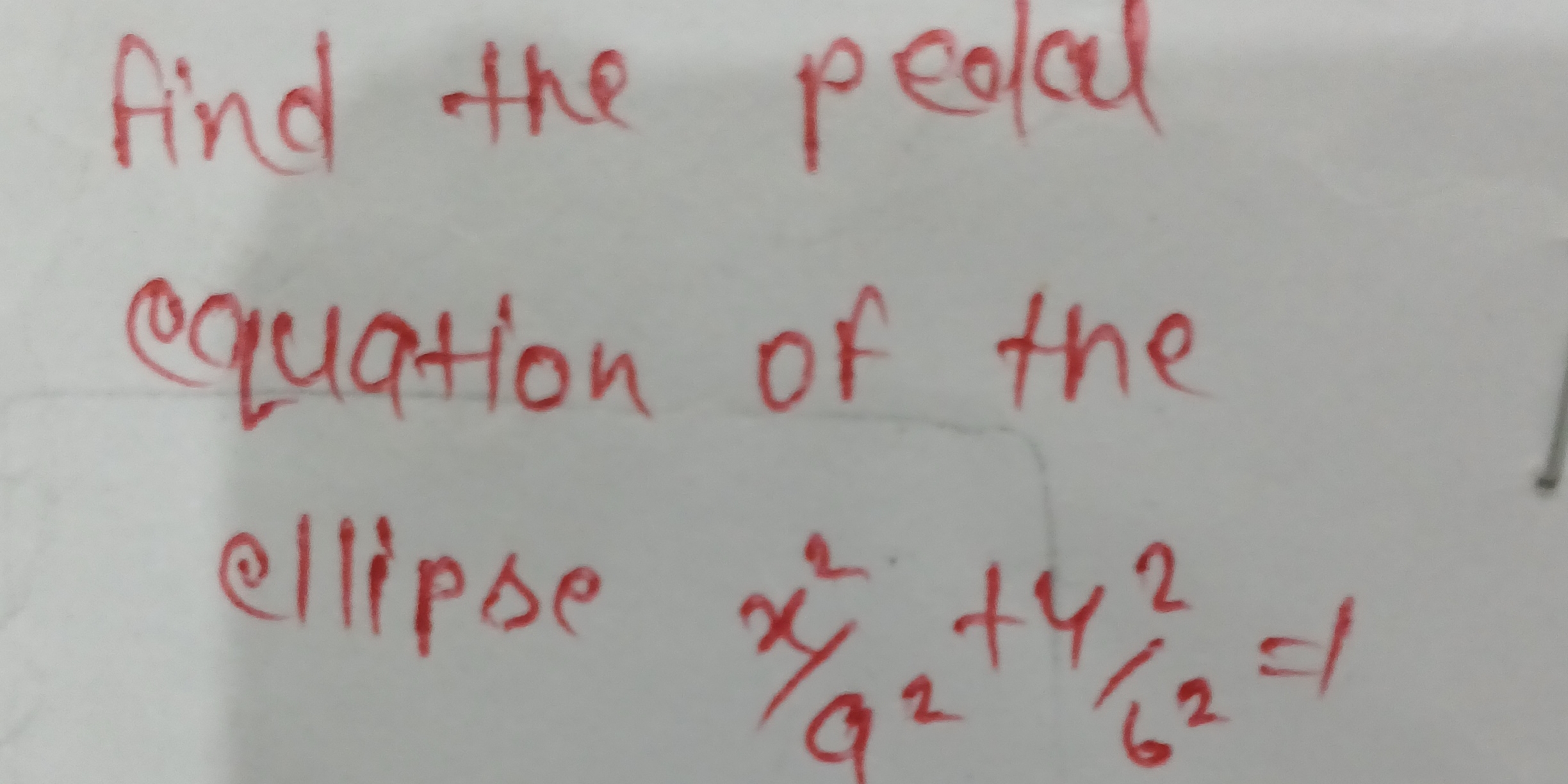
Understand the Problem
The question is asking to find the pedal equation of an ellipse defined by the equation mentioned. This involves using the properties of the ellipse and calculus to derive the pedal coordinates.
Answer
The pedal equation is given by: $$ r = \frac{24}{\sqrt{4 \sin^2 t + 36 \cos^2 t}} $$
Answer for screen readers
The pedal equation of the ellipse is:
$$ r = \frac{24}{\sqrt{4 \sin^2 t + 36 \cos^2 t}} $$
Steps to Solve
- Identify the ellipse parameters
The given ellipse equation is
$$ \frac{x^2}{4} + \frac{y^2}{36} = 1 $$
From this, we can identify the semi-major axis $a = 6$ and the semi-minor axis $b = 2$.
- Convert to parametric equations
The parametric equations for the ellipse can be represented as:
$$ x = a \cos t = 2 \cos t $$
$$ y = b \sin t = 6 \sin t $$
where $t$ is the parameter.
- Determine the derivatives
We need to calculate the derivatives of $x$ and $y$ with respect to $t$:
$$ \frac{dx}{dt} = -2 \sin t $$
$$ \frac{dy}{dt} = 6 \cos t $$
- Calculate the slope of the tangent line
The slope of the tangent line at a point on the ellipse is given by:
$$ \frac{dy}{dx} = \frac{dy/dt}{dx/dt} $$
Substituting the derivatives we found:
$$ \frac{dy}{dx} = \frac{6 \cos t}{-2 \sin t} = -3 \cot t $$
- Find the pedal formula
The pedal distance $r$ from the directrix to the curve is given by the formula:
$$ r = \frac{b^2}{\sqrt{(dx/dt)^2 + (dy/dt)^2}} $$
Calculating the distance:
- First, find $(dx/dt)^2 + (dy/dt)^2$:
$$ (dx/dt)^2 + (dy/dt)^2 = (-2 \sin t)^2 + (6 \cos t)^2 = 4 \sin^2 t + 36 \cos^2 t $$
- Thus, we have:
$$ r = \frac{4 \cdot 36}{\sqrt{4 \sin^2 t + 36 \cos^2 t}} $$
Simplifying this expression gives you the final pedal equation.
- Combine terms for the final expression
The above expression provides the pedal equation as a function of $t$, using trigonometric identities as necessary to simplify.
The pedal equation of the ellipse is:
$$ r = \frac{24}{\sqrt{4 \sin^2 t + 36 \cos^2 t}} $$
More Information
The pedal equation gives a relationship between the radius $r$ (the distance from the focal point to the tangent line at the point on the ellipse) and the angle $t$. It effectively expresses how the distance changes as we move along the ellipse.
Tips
- Incorrectly identifying the semi-major and semi-minor axes: Ensure that $a$ and $b$ are assigned correctly depending on their values in the standard form of the ellipse.
- Miscalculating the derivatives: Double-check the calculations for $dx/dt$ and $dy/dt$ to ensure accuracy.
AI-generated content may contain errors. Please verify critical information