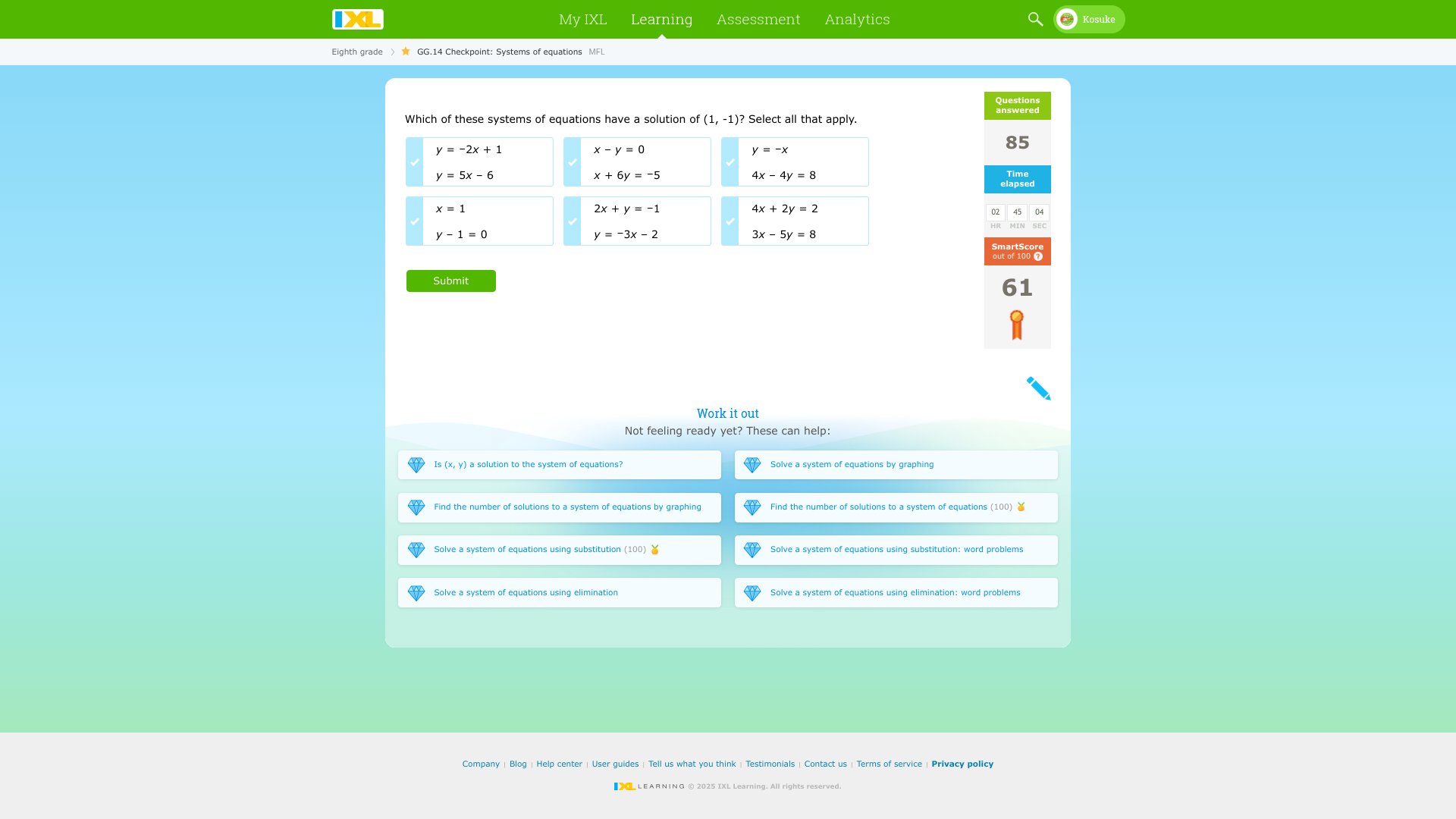
Which of these systems of equations have a solution of (1, -1)? Select all that apply.

Understand the Problem

The question is asking which given systems of equations have the specific solution of (1, -1). It requires the user to evaluate each equation to determine if it holds true for that specific solution.

Answer

The systems that have the solution of (1, -1) are $ y = -2x + 1 $, $ y = 5x - 6 $, $ y = -x $, $ x + 6y = -5 $, $ 4x - 4y = 8 $, $ 4x + 2y = 2 $, and $ 3x - 5y = 8 $.

Steps to Solve

Identify the System of Equations We need to check each system of equations to see if the point (1, -1) satisfies them.
Evaluate Each Equation Substitute ( x = 1 ) and ( y = -1 ) into each equation.
Equation Evaluation
- For the equation ( y = -2x + 1 ): $$ -1 = -2(1) + 1 $$ This simplifies to ( -1 = -2 + 1 ), which is true since ( -1 = -1 ).
- For the equation ( y = 5x - 6 ): $$ -1 = 5(1) - 6 $$ This simplifies to ( -1 = 5 - 6 ), which is also true since ( -1 = -1 ).
- For the equation ( x - y = 0 ): $$ 1 - (-1) = 0 $$ This simplifies to ( 1 + 1 = 0 ), which is false since ( 2 \neq 0 ).
- For the equation ( y = -x ): $$ -1 = -1 $$ This is true since both sides are equal.
- For the equation ( x + 6y = -5 ): $$ 1 + 6(-1) = -5 $$ This simplifies to ( 1 - 6 = -5 ), which is true since ( -5 = -5 ).
- For the equation ( 4x - 4y = 8 ): $$ 4(1) - 4(-1) = 8 $$ This simplifies to ( 4 + 4 = 8 ), which is true since ( 8 = 8 ).
- For the equation ( 2x + 2y = -1 ): $$ 2(1) + 2(-1) = -1 $$ This simplifies to ( 2 - 2 = -1 ), which is false since ( 0 \neq -1 ).
- For the equation ( y = -3x - 2 ): $$ -1 = -3(1) - 2 $$ This simplifies to ( -1 = -3 - 2 ), which is false since ( -1 \neq -5 ).
- For the equation ( 4x + 2y = 2 ): $$ 4(1) + 2(-1) = 2 $$ This simplifies to ( 4 - 2 = 2 ), which is true since ( 2 = 2 ).
- For the equation ( 3x - 5y = 8 ): $$ 3(1) - 5(-1) = 8 $$ This simplifies to ( 3 + 5 = 8 ), which is true since ( 8 = 8 ).
Compile the Results The equations that hold true for the solution (1, -1) are:
- ( y = -2x + 1 )
- ( y = 5x - 6 )
- ( y = -x )
- ( x + 6y = -5 )
- ( 4x - 4y = 8 )
- ( 4x + 2y = 2 )
- ( 3x - 5y = 8 )

The valid systems of equations are:

( y = -2x + 1 )
( y = 5x - 6 )
( y = -x )
( x + 6y = -5 )
( 4x - 4y = 8 )
( 4x + 2y = 2 )
( 3x - 5y = 8 )

More Information

The solution (1, -1) indicates that this point lies on the lines represented by the equations. When substituting the values of ( x ) and ( y ) into the equations confirms which equations contain this point.

Tips

Not substituting both ( x ) and ( y ) into each equation correctly.
Simplifying incorrectly or making arithmetic errors during substitution.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!