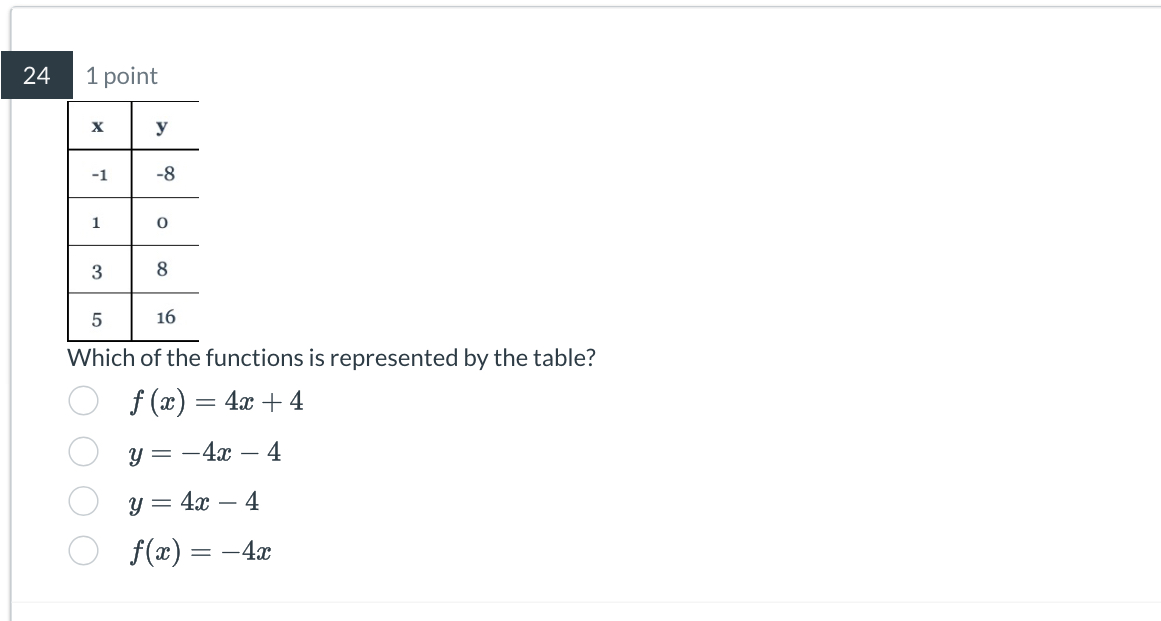
Which of the functions is represented by the table?

Steps to Solve

1. Identify the function type

First, we note that we are looking for a linear function of the form $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept. We will calculate the slope using two points from the table.

2. Calculate the slope (m)

Using points (-1, -8) and (1, 0):

The formula for slope is:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Substituting the values:

$$ m = \frac{0 - (-8)}{1 - (-1)} = \frac{0 + 8}{1 + 1} = \frac{8}{2} = 4 $$

3. Find the y-intercept (b)

Next, we use one of the points (1, 0) and the slope $m = 4$ to find $b$.

Using the equation $y = mx + b$:

$$ 0 = 4(1) + b $$

Solving for $b$ gives:

$$ b = 0 - 4 = -4 $$

So, the function is:

$$ y = 4x - 4 $$

4. Check against the options

Now we compare our derived function $y = 4x - 4$ with the given options.

• $f(x) = 4x + 4$ (not correct)
• $y = -4x - 4$ (not correct)
• $y = 4x - 4$ (correct)
• $f(x) = -4x$ (not correct)

5. Verify with the table of values

Finally, we can check if our function $y = 4x - 4$ satisfies all points in the table:

For $x = -1$: $$ y = 4(-1) - 4 = -4 - 4 = -8 $$

For $x = 1$: $$ y = 4(1) - 4 = 0 $$

For $x = 3$: $$ y = 4(3) - 4 = 12 - 4 = 8 $$

For $x = 5$: $$ y = 4(5) - 4 = 20 - 4 = 16 $$

All values match with the table.