Which of the following inequalities is graphed on the coordinate plane?
Understand the Problem
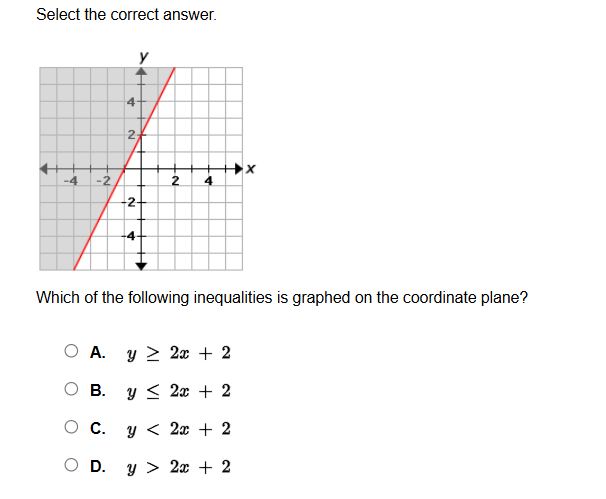
The question is asking which inequality is represented by the red line graphed on the coordinate plane. We need to determine the slope and y-intercept of the line to identify the correct inequality from the provided options.
Answer
The correct inequality is \(y > 2x + 2\).
Answer for screen readers
The correct inequality is (y > 2x + 2).
Steps to Solve
- Identify the slope and y-intercept of the line
From the graph, it appears the line intersects the y-axis at (2) and has a slope of (2). This means the equation of the line in slope-intercept form is: $$y = 2x + 2$$
- Determine the type of line (dashed or solid)
Since the line is solid (not dashed), it indicates that the points on the line are included in the inequality.
- Analyze the shading of the graph
The shaded area is above the line. This suggests that the inequality is of the form where (y) is greater than the line equation: $$y > 2x + 2$$
- Select the correct inequality from the options
Considering our findings, we confirm that this matches option D: $$y > 2x + 2$$
The correct inequality is (y > 2x + 2).
More Information
The slope of the line indicates the steepness, while the y-intercept is the point where the line crosses the y-axis. Here, (2) is both the slope and the y-intercept. The solid line indicates that the boundary (the line itself) is included in the solution set.
Tips
- Confusing the direction of the inequality based on the shading of the graph. Always confirm the shading direction relative to the line.
- Misidentifying the slope or y-intercept from the graph, especially if coordinates are not read carefully.
