Which of the following combinations has the dimension of electrical resistance (ε0 is the permittivity of vacuum and μ0 is the permeability of vacuum)?
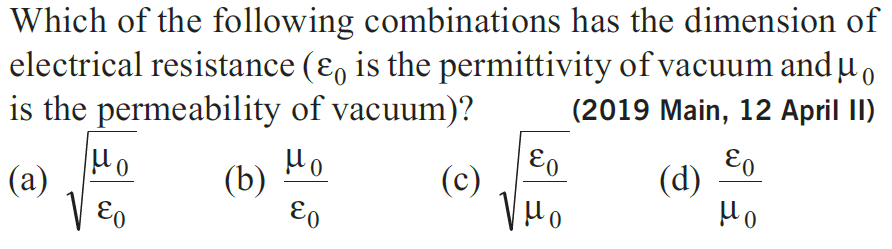
Understand the Problem
The question is asking which of the provided combinations of the permittivity and permeability of vacuum corresponds to the dimension of electrical resistance.
Answer
The combination that has the dimension of electrical resistance is \( \sqrt{\frac{\mu_0}{\epsilon_0}} \).
Answer for screen readers
The correct combination that has the dimension of electrical resistance is option (a):
$$ \sqrt{\frac{\mu_0}{\epsilon_0}} $$
Steps to Solve
-
Identify the dimensions of permittivity and permeability
The permittivity of vacuum ($\epsilon_0$) has the dimension of capacitance per unit length, which is given by: $$ [\epsilon_0] = \frac{[C^2]}{[N \cdot m^2]} = \frac{[Q^2]}{[M \cdot L^2 \cdot T^{-4}]} $$
The permeability of vacuum ($\mu_0$) has the dimension of inductance per unit length: $$ [\mu_0] = \frac{[N \cdot s^2]}{[C^2]} = \frac{[M \cdot L]}{[T^2 \cdot Q^2]} $$
-
Express the dimensions of electrical resistance
The electrical resistance ($R$) has the dimension: $$ [R] = \frac{[V]}{[I]} = \frac{[M \cdot L^2 \cdot T^{-3}]}{[Q]} $$
-
Evaluate each option
Compute the dimensions for each option and check for dimensional equivalence with resistance.
-
Option (a): $$ \sqrt{\frac{\mu_0}{\epsilon_0}} = \sqrt{\frac{\frac{[M \cdot L]}{[T^2 \cdot Q^2]}}{\frac{[Q^2]}{[M \cdot L^2 \cdot T^{-4}]}}} = \sqrt{\frac{[M \cdot L^3 \cdot T^{-4}]}{[Q^4]}} $$
-
Option (b): $$ \frac{\mu_0}{\epsilon_0} = \frac{\frac{[M \cdot L]}{[T^2 \cdot Q^2]}}{\frac{[Q^2]}{[M \cdot L^2 \cdot T^{-4}]}} = \frac{[M^2 \cdot L^3 \cdot T^{-4}]}{[Q^4]} $$
-
Option (c): $$ \sqrt{\frac{\epsilon_0}{\mu_0}} = \sqrt{\frac{\frac{[Q^2]}{[M \cdot L^2 \cdot T^{-4}]}}{\frac{[M \cdot L]}{[T^2 \cdot Q^2]}}} = \sqrt{\frac{[Q^4]}{[M^2 \cdot L^3 \cdot T^{-2}]}} $$
-
Option (d): $$ \frac{\epsilon_0}{\mu_0} = \frac{\frac{[Q^2]}{[M \cdot L^2 \cdot T^{-4}]}}{\frac{[M \cdot L]}{[T^2 \cdot Q^2]}} = \frac{[Q^4 \cdot T^2]}{[M^2 \cdot L^3]} $$
-
-
Select the correct option
Identify which of the derived expressions matches the dimension of electrical resistance.
The correct combination that has the dimension of electrical resistance is option (a):
$$ \sqrt{\frac{\mu_0}{\epsilon_0}} $$
More Information
The relationship between permittivity and permeability in a vacuum is essential in understanding electromagnetic waves, where the speed of light $c$ is given by (c = \frac{1}{\sqrt{\epsilon_0 \mu_0}}). The dimensions of resistance also connect to charge and energy concepts in physics.
Tips
- Confusing the dimensions of permittivity and permeability.
- Neglecting to simplify the expressions properly when calculating combinations.
AI-generated content may contain errors. Please verify critical information