Trong hệ trục tọa độ Oxyz, cho ba điểm A(2;-1;3) và C(-2;6;-3). Tính h(a+b-c) với (a;b;c) là tọa độ của AM.
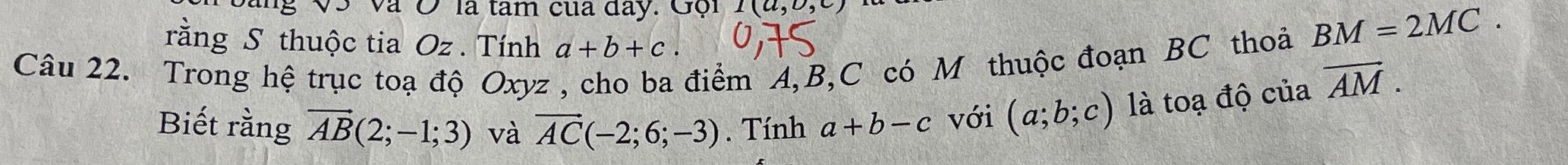
Understand the Problem
Câu hỏi yêu cầu tính toán liên quan đến hệ trục tọa độ không gian và ba điểm A, B, C. Chúng ta cần xác định độ dài các đoạn thẳng và mối quan hệ giữa chúng trong hệ tọa độ xyz.
Answer
$$ a + b - c = \frac{16}{3} $$
Answer for screen readers
$$ a + b - c = \frac{16}{3} $$
Steps to Solve
- Định nghĩa tọa độ các điểm A, B, C
Cho các điểm A, B, C như sau:
- Điểm A có tọa độ ( A(2, -1, 3) )
- Điểm B có tọa độ ( B(0, 7, 5) )
- Điểm C có tọa độ ( C(-2, 6, -3) )
- Tính độ dài đoạn thẳng AB
Sử dụng công thức tính độ dài đoạn thẳng giữa hai điểm trong không gian: [ d_{AB} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2 + (z_B - z_A)^2} ]
Áp dụng vào tọa độ: [ d_{AB} = \sqrt{(0 - 2)^2 + (7 - (-1))^2 + (5 - 3)^2} = \sqrt{(2)^2 + (8)^2 + (2)^2} = \sqrt{4 + 64 + 4} = \sqrt{72} = 6\sqrt{2} ]
- Tính độ dài đoạn thẳng AC
Áp dụng công thức tương tự cho đoạn thẳng AC: [ d_{AC} = \sqrt{(x_C - x_A)^2 + (y_C - y_A)^2 + (z_C - z_A)^2} ] [ d_{AC} = \sqrt{(-2 - 2)^2 + (6 - (-1))^2 + (-3 - 3)^2} = \sqrt{(-4)^2 + (7)^2 + (-6)^2} ] [ d_{AC} = \sqrt{16 + 49 + 36} = \sqrt{101} ]
- Sử dụng tỷ lệ BM = 2MC
Theo đề bài, cho M là điểm nằm trên đoạn BC sao cho ( BM = 2MC ). Điều này có nghĩa là ( \frac{BM}{MC} = 2 ), tức là M chia đoạn BC theo tỉ lệ 2:1.
- Tính tọa độ điểm M
Sử dụng công thức tìm tọa độ điểm chia đoạn thẳng theo tỉ lệ: [ M = \left( \frac{2x_C + x_B}{2 + 1}, \frac{2y_C + y_B}{2 + 1}, \frac{2z_C + z_B}{2 + 1} \right) ]
Tính tọa độ M: [ M = \left( \frac{2(-2) + 0}{3}, \frac{2(6) + 7}{3}, \frac{2(-3) + 5}{3} \right) ] [ = \left( \frac{-4}{3}, \frac{12 + 7}{3}, \frac{-6 + 5}{3} \right) = \left( -\frac{4}{3}, \frac{19}{3}, -\frac{1}{3} \right) ]
- Tính dấu hiệu ( a + b - c )
Cuối cùng, tính ( a + b - c ) từ tọa độ M:
- ( a = -\frac{4}{3} )
- ( b = \frac{19}{3} )
- ( c = -\frac{1}{3} )
Tính: [ a + b - c = -\frac{4}{3} + \frac{19}{3} - \left(-\frac{1}{3}\right) = -\frac{4}{3} + \frac{19}{3} + \frac{1}{3} = \frac{16}{3} ]
$$ a + b - c = \frac{16}{3} $$
More Information
Kết quả tính toán cung cấp giá trị cụ thể cho biểu thức ( a + b - c ), liên quan đến vị trí của điểm M trong không gian 3 chiều. Tỷ lệ chia đoạn BC là một ứng dụng thực tế của xác suất.
Tips
- Quên tính toán tọa độ M: Đôi khi, người học có thể bỏ qua bước tính tọa độ điểm chia đoạn thẳng theo tỷ lệ.
- Nhầm lẫn công thức: Sử dụng sai công thức tính độ dài đoạn thẳng hoặc tính sai khi quy đổi hệ tọa độ.
AI-generated content may contain errors. Please verify critical information