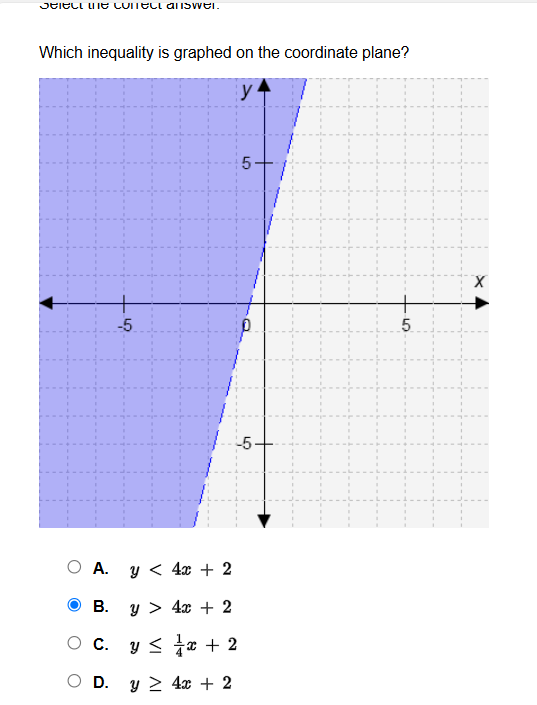
Which inequality is graphed on the coordinate plane?
Understand the Problem
The question is asking to identify which inequality corresponds to the shaded region on the coordinate plane. This involves understanding the representation of inequalities on a graph and what the shaded area signifies in relation to the line depicted.
Answer
$$y > 4x + 2$$
Answer for screen readers
The correct inequality graphed on the coordinate plane is:
$$y > 4x + 2$$
Steps to Solve
-
Identify the line equation
First, observe the boundary line in the graph. It appears to have a positive slope and crosses the y-axis above the origin. To determine the equation of this line, we can note it's similar to the form $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept. -
Determine the slope and intercept
By analyzing the graph, we can identify that the line has a slope of 4 and crosses the y-axis at 2. This gives us the equation of the line:
$$y = 4x + 2$$ -
Analyze the shaded region
The shaded area above the line indicates a greater-than inequality. Since the region above the line is shaded, the correct form of the inequality is:
$$y > 4x + 2$$ -
Select the correct inequality
Now, comparing with the options provided:
- A: $y < 4x + 2$ (incorrect)
- B: $y > 4x + 2$ (correct)
- C: $y \leq \frac{1}{4}x + 2$ (incorrect)
- D: $y \geq 4x + 2$ (incorrect)
The correct answer is B.
The correct inequality graphed on the coordinate plane is:
$$y > 4x + 2$$
More Information
The inequality $y > 4x + 2$ represents all the points in the coordinate plane that lie above the line $y = 4x + 2$. This line itself has a slope of 4, which means for every unit you move to the right, you move up 4 units.
Tips
Common mistakes include misidentifying the slope or confusing the direction of the inequality based on the shaded region. Always pay attention to whether the shaded area is above or below the line to determine the correct inequality sign.