Which inequality best represents the range of the function?
Understand the Problem
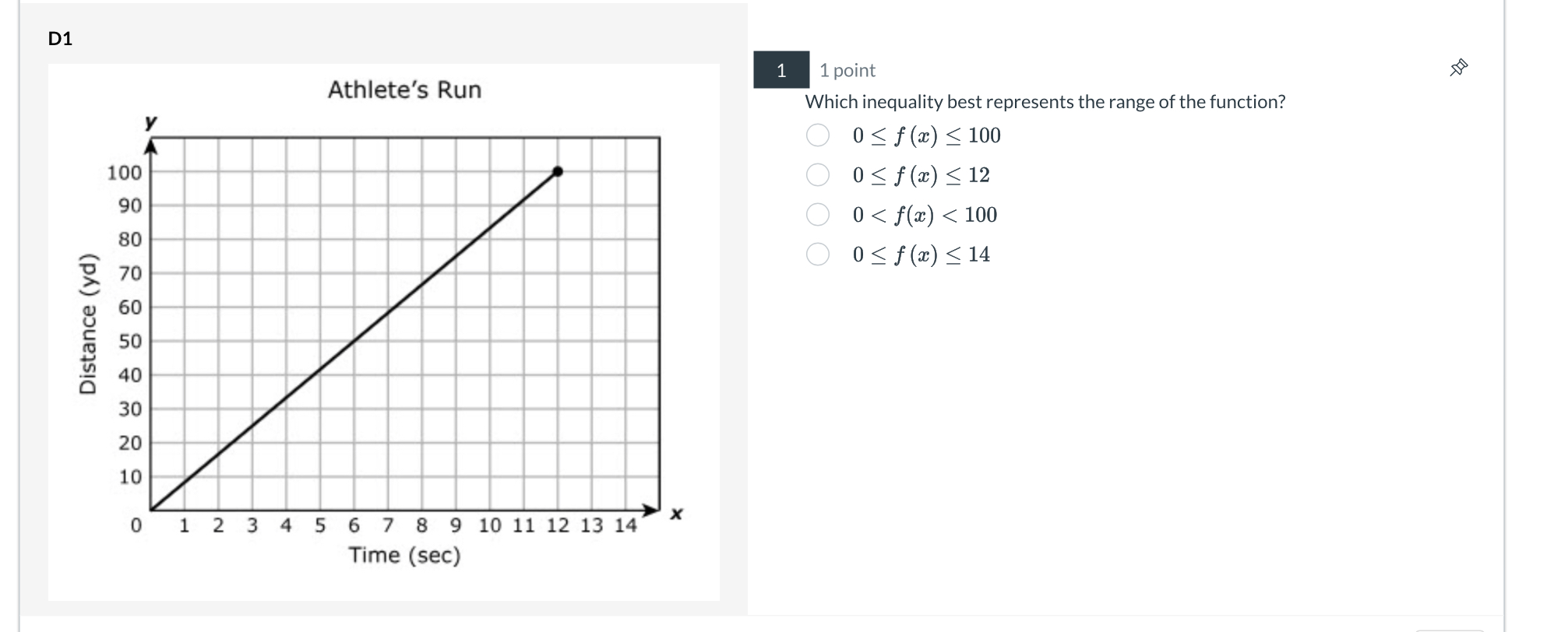
The question is asking which inequality appropriately describes the range of the function represented by the distance covered by an athlete over time, as illustrated in the accompanying graph.
Answer
The appropriate inequality is $0 \leq f(x) \leq 100$.
Answer for screen readers
The inequality that best represents the range of the function is:
$$0 \leq f(x) \leq 100$$
Steps to Solve
-
Identify the Range on the Graph
Look at the graph to determine the maximum distance reached by the athlete and the minimum distance. The graph shows the distance against time. -
Determine Maximum Distance
Observe that the maximum distance reached on the vertical axis (distance in yards) is 100 yards. -
Determine Minimum Distance
The minimum distance is where the graph starts on the vertical axis. In this case, it starts at 0 yards. -
Construct the Inequality
Using the identified maximum and minimum distances, write the inequality that represents the range of the function. The inequality will be $0 \leq f(x) \leq 100$.
The inequality that best represents the range of the function is:
$$0 \leq f(x) \leq 100$$
More Information
This indicates that the athlete covers a distance starting from 0 yards up to a maximum of 100 yards during the time period shown on the graph.
Tips
Common mistakes include:
- Misreading the graph and incorrectly identifying the maximum or minimum distance.
- Assuming the athlete travels less than the maximum shown without checking the graph.
AI-generated content may contain errors. Please verify critical information