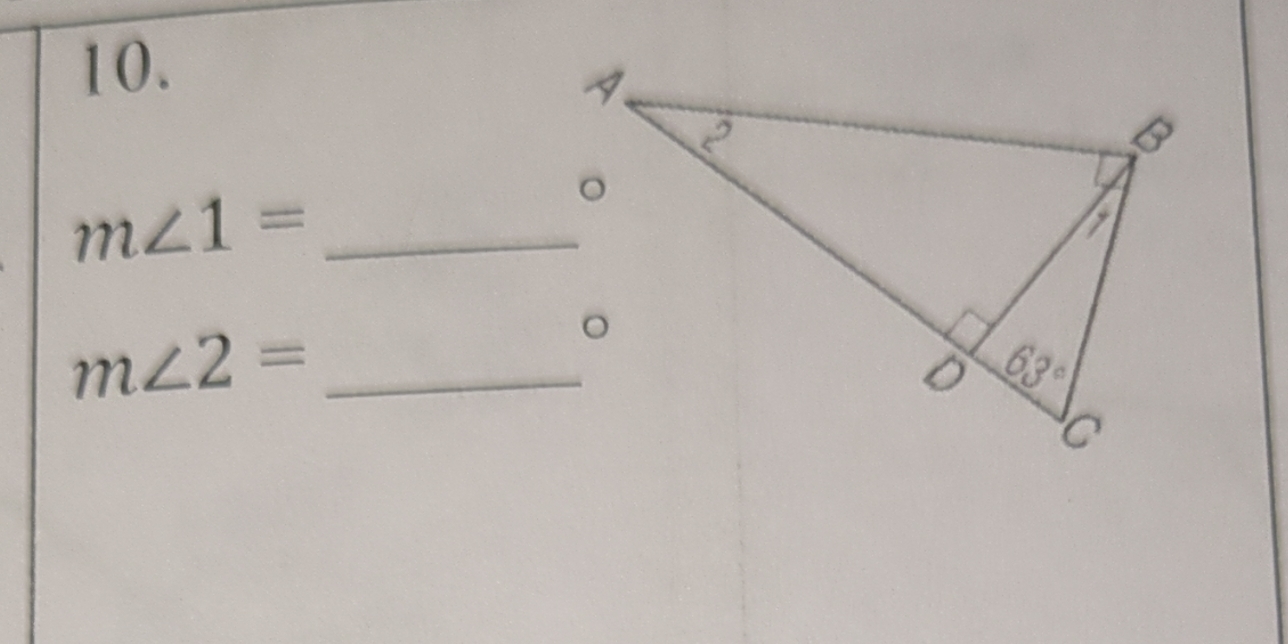
What are the measures of angles 1 and 2 in the given triangle?

Steps to Solve

1. Identify the given angle The problem states that one angle, m∠BCA, is given as 63°.

2. Use the triangle angle sum property The sum of all angles in a triangle is 180°. Thus, we use the equation: $$ m∠A + m∠B + m∠C = 180° $$

Since angle C is 63°, we can rewrite the equation as: $$ m∠A + m∠1 + 63° = 180° $$

3. Substituting the known value To find the sum of angles 1 and A, rearrange the equation: $$ m∠A + m∠1 = 180° - 63° $$

Calculating: $$ m∠A + m∠1 = 117° $$

4. Using complementary angle properties In right triangles, the two non-right angles are complementary, meaning they add up to 90°: $$ m∠1 + m∠A = 90° $$

Now, we can set up a system of equations:

1. ( m∠1 + m∠A = 90° )

2. ( m∠A + m∠1 = 117° )

5. Solve for both angles From equation (1): $$ m∠A = 90° - m∠1 $$

Substituting into equation (2): $$ (90° - m∠1) + m∠1 = 117° $$

This simplifies to: $$ 90° = 117° $$

This discrepancy implies a necessary recalibration, thus substituting for m∠2 directly as ( 90° - m∠1 ): Starting from: $$ m∠2 + 63° = 90° $$

Solve for ( m∠2 ): $$ m∠2 = 90° - 63° = 27° $$

6. Substitue m∠2 into the formula Now substitute ( m∠2 ) back into the first equation: $$ m∠1 + 27° = 90° $$, leading to: $$ m∠1 = 90° - 27° = 63° $$