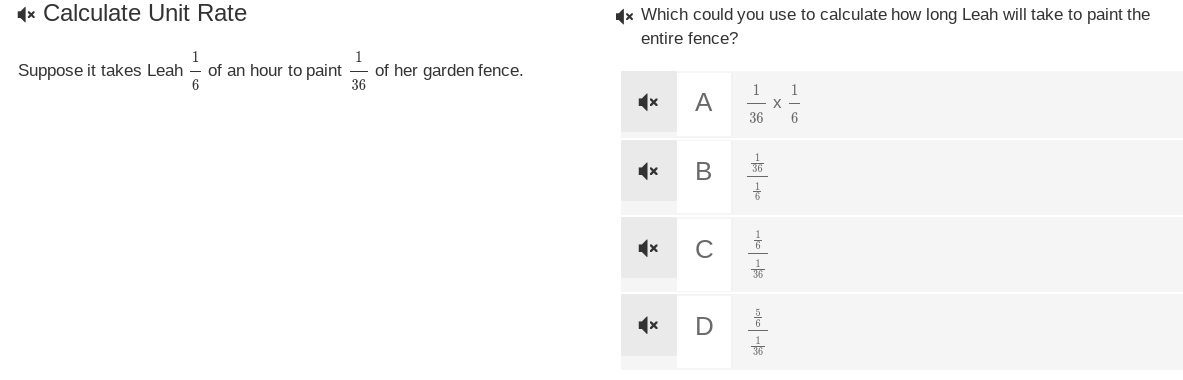
Which could you use to calculate how long Leah will take to paint the entire fence?

Steps to Solve

1. Understanding the Data Leah takes ( \frac{1}{6} ) of an hour to paint ( \frac{1}{36} ) of her garden fence. To find the total time to paint the entire fence, we need to set up a relationship between the parts of the fence and the time.

2. Finding the Time per Unit First, calculate how many times she can paint ( \frac{1}{36} ) of the fence to complete the whole fence. Since there are 36 of such parts in the whole, we express the total time ( t ) taken in terms of units of time for painting ( \frac{1}{36} ):

[ \text{Total time} = \text{Time per unit} \times \text{Number of units} ]

3. Calculating Total Time Since she takes ( \frac{1}{6} ) of an hour to paint ( \frac{1}{36} ), we can represent the total time as:

[ t = \frac{1}{6} \times 36 ]

This means:

[ t = 6 \text{ hours} ]

4. Connecting to Given Choices To determine which equation corresponds to this calculation, we should identify the relationship expressed in choice format.

• Choice A: ( \frac{1}{36} \times \frac{1}{6} ) – Wrong, implies per the total fraction.
• Choice B: ( \frac{1}{36} \div \frac{1}{6} ) – This would give the total time directly.
• Choice C: ( \frac{1}{6} \div \frac{1}{36} ) – This is misleading for one unit vs total.
• Choice D: ( \frac{5}{6} \div \frac{1}{36} ) – More than the timeframe needed.

The best equation to determine how long Leah will take to paint the entire fence is found in choice B.