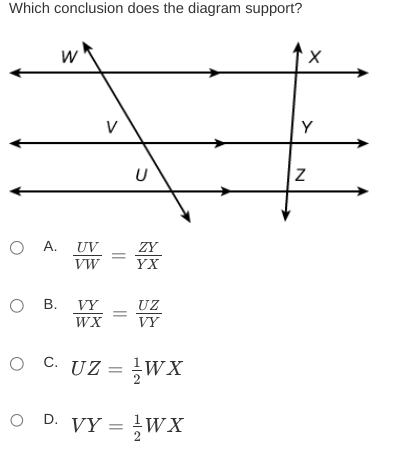
Which conclusion does the diagram support?

Steps to Solve

1. Identify the relationship in the diagram

The diagram illustrates two parallel lines (segments $VW$ and $XZ$) cut by transversal lines (segments $WY$ and $UZ$). According to the properties of parallel lines cut by a transversal, the ratios of the segments will be equal.

2. Use the corresponding segments

From the diagram, we can set up the following ratios based on the segments:

• The segment $UV$ is to $VW$ as segment $ZY$ is to $YX$.

Thus, we can express this relationship as:

$$ \frac{UV}{VW} = \frac{ZY}{YX} $$

3. Verify each option

Let's check each conclusion against our established relationship.

• Option A: $UV/VW = ZY/YX$ matches our relationship.
• Option B: $VY/WX = UZ/VY$ does not relate to the segments.
• Option C: $UZ = \frac{1}{2}WX$ cannot be directly inferred without specific segment lengths.
• Option D: $VY = \frac{1}{2}WX$ cannot be inferred directly without knowing relationships.

4. Conclusion on supported option

Since Option A aligns perfectly with the identified relationship established by the parallel lines and transversals, it is supported by the diagram.