20/7 ÷ (-12/35)
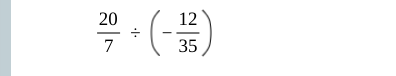
Understand the Problem
The question is asking us to perform the division of two fractions: 20/7 divided by -12/35. The high-level approach involves converting the division to multiplication by the reciprocal of the second fraction and then simplifying the result.
Answer
The answer is $-\frac{25}{3}$.
Answer for screen readers
The final simplified answer is: $$ -\frac{25}{3} $$
Steps to Solve
- Convert Division to Multiplication To divide by a fraction, multiply by its reciprocal. The reciprocal of $-\frac{12}{35}$ is $-\frac{35}{12}$.
The expression now becomes: $$ \frac{20}{7} \times \left(-\frac{35}{12}\right) $$
- Multiply the Numerators and Denominators Multiply the numerators together and the denominators together: $$ \text{Numerator: } 20 \times (-35) = -700 $$ $$ \text{Denominator: } 7 \times 12 = 84 $$
So we have: $$ \frac{-700}{84} $$
- Simplify the Fraction To simplify $\frac{-700}{84}$, find the greatest common divisor (GCD) of 700 and 84. The GCD is 4.
Now divide both the numerator and denominator by 4: $$ \frac{-700 \div 4}{84 \div 4} = \frac{-175}{21} $$
- Final Check for Further Simplification Check to see if $\frac{-175}{21}$ can be simplified further. The GCD of 175 and 21 is 7.
Divide both numbers by 7: $$ \frac{-175 \div 7}{21 \div 7} = \frac{-25}{3} $$
The final simplified answer is: $$ -\frac{25}{3} $$
More Information
In the division of fractions, it’s important to remember to multiply by the reciprocal of the fraction you are dividing by. This approach simplifies the process and often results in cleaner computations.
Tips
- Not flipping the second fraction: A common mistake is forgetting to take the reciprocal of the divisor. Always remember to change division into multiplication by the reciprocal.
- Improper simplification: Ensure you check for simplicity at each step, and use the GCD effectively to arrive at the simplest form.
AI-generated content may contain errors. Please verify critical information