Where is A' if A is translated <3, -2>?
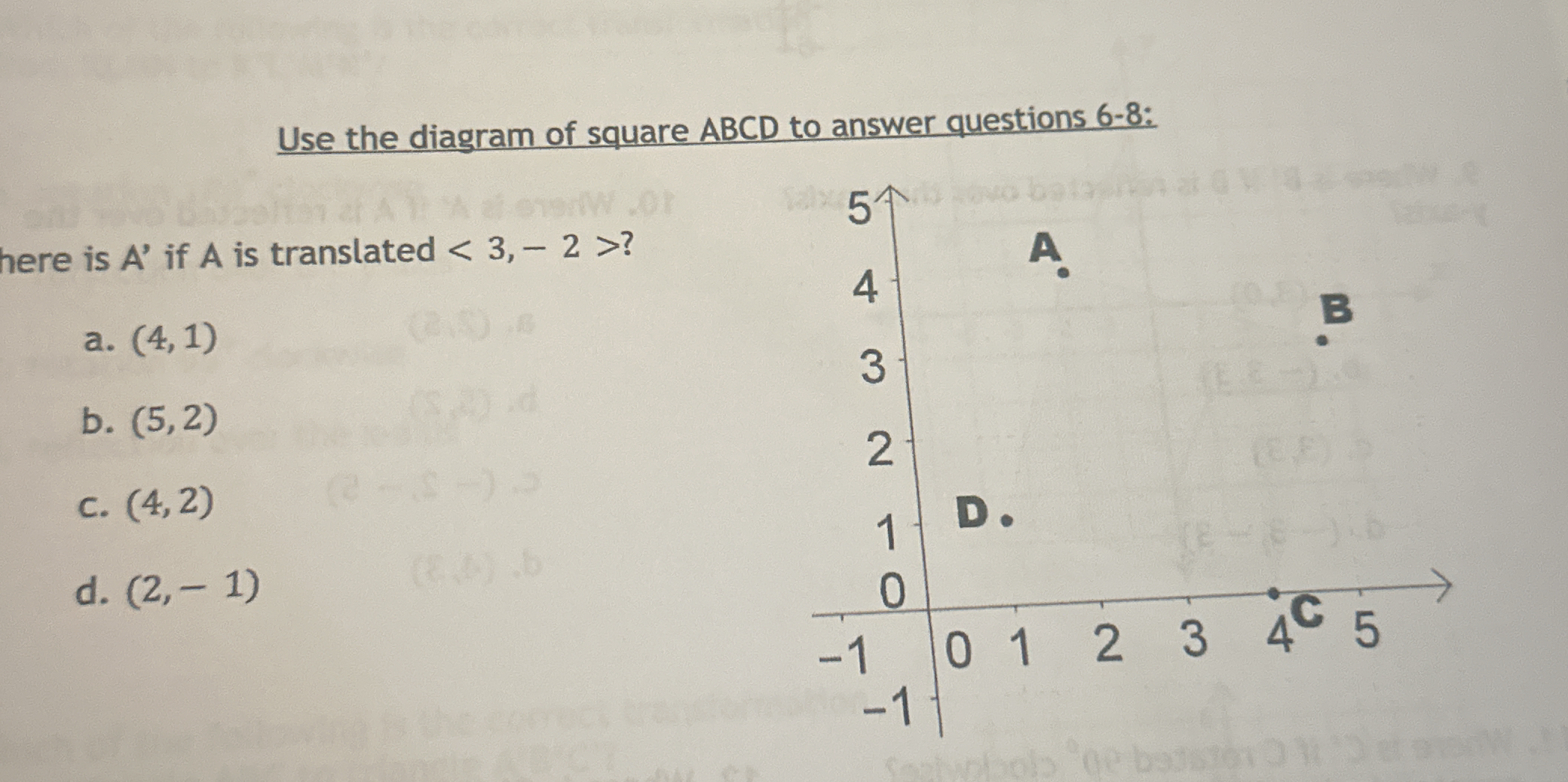
Understand the Problem
The question is asking for the new coordinates of point A after applying a translation of <3, -2> to its original location. We need to find point A's new coordinates among the provided options after the translation is performed.
Answer
The new coordinates after translation are $(4, 1)$.
Answer for screen readers
The new coordinates of point A after translation are (4, 1).
Steps to Solve
-
Identify the original coordinates of point A From the diagram, the coordinates of point A are given as (1, 3).
-
Apply the translation vector The translation vector is <3, -2>. This means we will add 3 to the x-coordinate and subtract 2 from the y-coordinate.
New x-coordinate: $$ 1 + 3 = 4 $$
New y-coordinate: $$ 3 - 2 = 1 $$
-
Write the new coordinates After applying the translation, the new coordinates of point A (denoted as A') are (4, 1).
-
Compare the new coordinates with the options The options given are:
- a. (4, 1)
- b. (5, 2)
- c. (4, 2)
- d. (2, -1)
We can see that the new coordinates (4, 1) match option a.
The new coordinates of point A after translation are (4, 1).
More Information
The operation performed here is a translation, which involves moving a point in a coordinate system a certain distance in the x and y directions. This is a fundamental concept in geometry, especially when working with transformations of shapes on a coordinate plane.
Tips
- Misunderstanding the translation vector: Remember that the first number in the translation vector affects the x-coordinate and the second number affects the y-coordinate.
- Forgetting to either add or subtract the values from the coordinates. It's crucial to keep track of the signs given in the translation vector.
AI-generated content may contain errors. Please verify critical information